ARC066 D. Xor Sum

問題

正の整数Nが与えられる。
ここで、2つの整数0 <= u, v <= Nであって、ある非負整数a,bが存在して、a ^ b = u, a + b = vとなるものが何通りあるか求めよ。
答えは1,000,000,007のあまりを答えよ。
上記の^はビットごとの排他的論理和を表す。

制約

• 1 <= N <= 10^18

解法

まだイマイチ理解できていないところが残っているけど、とりあえずまとめ。
制約が非常に大きく、xorがビットごとの計算でもあるので、ビットの桁DPを考える。
以下、解説放送から。(下から桁DP)

問題がやや扱いにくいので、言い換えを考える。
a,bを用いた制約があるので、結局「(a xor b, a+b)が何通りあるか？」という話でであるが、aとbが入れ替わったものを重複しないように数え上げる必要がある。
重複する部分は、各bitがa側とb側で入れ替わったとしても最終的な結果には変わらない部分のことで、「a側が1、b側が0」の場合と「a側が0、b側が1」の場合、２重カウントしてしまう。
これを片方だけカウントするようにするため、「(a xor b, a+b)が何通りあるか？ただし、各ビットについて、(a側のビット,b側のビット)=(0,0)(1,0)(1,1)のものだけ考える」という問題に言い換える。

func(S,X):=「a+b<=S」「a^b<=X」のとき、各ビットが(0,0)(1,0)(1,1)のものだけ考えた場合の、答えの通り数」
と考えると、aとbの一番右側のビットについて、上記の3パターンで場合分けをする。
(1) aとbの一番右側のビットが(0,0)の場合
a=2a', b=2b'と表現できるので、これで考えると、
a'+b' <= S/2
a' ^ b' <= X/2
なので、func(S/2, X/2)

(2) aとbの一番右側のビットが(1,0)の場合
a=2a'+1, b=2b'と表現できるので、これで考えると、
a'+b' <= (S-1)/2
a' ^ b' <= (X-1)/2
なので、func((S-1)/2, (X-1)/2)

(3) aとbの一番右側のビットが(1,1)の場合
a=2a'+1, b=2b'+1と表現できるので、これで考えると、
a'+b' <= (S-2)/2
a' ^ b' <= X/2
なので、func((S-2)/2, X/2)

となる。したがって、
func(S, X) = func(S/2, X/2) + func((S-1)/2, (X-1)/2) + func((S-2)/2, X/2)
となる。
SやXが0や1のときは1通り、0未満のときは0通りになることを注意してメモ化再帰を実装すればO(log N)程度で解ける。

解法2

解説PDFから。(上から桁DP)

まず、xorというのは「桁上りのない加算」といえるところから、a ^ bとa + bを比べた場合、
a + b = a ^ b + (1 << (a & b))
という条件から、a ^ b <= a + bなので、「vがN以下かどうか」だけを考えれば良いことがわかる。
したがって、この単純に制約をそのままDPを考えると、
dp[i][j] := 上からiビットまで決まっているとき、j=vとなる通り数
が考えられる。

このままだと、jの部分がNまで考える必要があり、N<=10^18なので、メモリが足りない。
ここで、jを「上からiビットまでの部分だけ」で考える。
jの条件をNについてひっくり返して、
dp[i][j] := 上からiビットまで決まっているとき、N-j=vとなる通り数
にすると、jは0以上かどうかを考えればよく、さらに上からiビットまでで考えるために、
dp[i][j] := 上からiビットまで決まっているとき、(N>>i)-j=(v>>i)となる通り数
というのを考える。

このdpは、上からi-1(dp[i+1][*])ビットまでがわかっていて、iビット目を考えるとき、dp[i+1][j]でのjはiビット目で考える場合は2倍になることに注意すると、
(1) Nの上からiビット目が0の場合
j=0は、
(aのiビット目,bのiビット目)=(0,0)のとき、dp[i+1][0]
(aのiビット目,bのiビット目)=(1,0)のとき、なし
(aのiビット目,bのiビット目)=(1,1)のとき、dp[i+1][1]
j=1は、
(aのiビット目,bのiビット目)=(0,0)のとき、なし
(aのiビット目,bのiビット目)=(1,0)のとき、dp[i+1][1]
(aのiビット目,bのiビット目)=(1,1)のとき、なし
j=2は、
(aのiビット目,bのiビット目)=(0,0)のとき、dp[i+1][1]
(aのiビット目,bのiビット目)=(1,0)のとき、なし
(aのiビット目,bのiビット目)=(1,1)のとき、dp[i+1][2]
j=3は、
(aのiビット目,bのiビット目)=(0,0)のとき、なし
(aのiビット目,bのiビット目)=(1,0)のとき、dp[i+1][2]
(aのiビット目,bのiビット目)=(1,1)のとき、なし
j=4は、
・・・

(2) Nの上からiビット目が1の場合
j=0は、
(aのiビット目,bのiビット目)=(0,0)のとき、なし
(aのiビット目,bのiビット目)=(1,0)のとき、dp[i+1][0]
(aのiビット目,bのiビット目)=(1,1)のとき、なし
j=1は、
(aのiビット目,bのiビット目)=(0,0)のとき、dp[i+1][0]
(aのiビット目,bのiビット目)=(1,0)のとき、なし
(aのiビット目,bのiビット目)=(1,1)のとき、dp[i+1][1]
j=2は、
(aのiビット目,bのiビット目)=(0,0)のとき、なし
(aのiビット目,bのiビット目)=(1,0)のとき、dp[i+1][1]
(aのiビット目,bのiビット目)=(1,1)のとき、なし
j=3は、
(aのiビット目,bのiビット目)=(0,0)のとき、dp[i+1][1]
(aのiビット目,bのiビット目)=(1,0)のとき、なし
(aのiビット目,bのiビット目)=(1,1)のとき、dp[i+1][2]
j=4は、
・・・

のような遷移になる。
上記の遷移は周期性があり、j=2以上のときは、j=2以上のところにしか遷移しないため、「2以上」というふうにまとめ上げて計算してもよい。
すると、j=0,1,2以上の3パターンだけ考えれば良く、上記の遷移をまとめあげると、
(1) Nの上からiビット目が0の場合
j=0は、dp[i][0] = dp[i+1][0] + dp[i+1][1]
j=1は、dp[i][1] = dp[i+1][1]
j=2以上は、dp[i][2以上] = dp[i+1][1] + dp[i+1][2以上] * 3

(2) Nの上からiビット目が1の場合
j=0は、dp[i][0] = dp[i+1][0]
j=1は、dp[i][1] = dp[i+1][0] + dp[i+1][1]
j=2以上は、dp[i][2以上] = dp[i+1][1] * 2 + dp[i+1][2以上] * 3

とすることができる。
答えはΣ_{j=0,1,2以上} dp[0][j]になる。
上記の計算をするだけなので、O(log N)程度で解ける。(MODを取るのを忘れずに)

その他

Xor Sum(ARC066 D)についてのいろんな解法 - Qiita

yukicoder No.749 クエリ全部盛り

問題

すべての要素が0で初期化された長さNの数列{a_i}が与えられる。
Q個のクエリが与えられるので、処理せよ。
各クエリ(q,l,r,k)はqの値に応じた処理を行うこと。

• q=0: k*Σ_{i=l}^r a_iのmod 10^9+7を出力
• q=1: l <= i <= rについて、a_iをkに変更
• q=2: l <= i <= rについて、a_iをa_i+kに変更
• q=3: l <= i <= rについて、a_iをa_i*kに変更
• q=4: l <= i <= rについて、a_iをa_i+k*F_iに変更
  • ただし、F_iはフィボナッチ数列のi番目の値

制約

• 1 <= N <= 10^6
• 0 <= Q <= 10^5
• 0 <= l <= r < N
• 0 <= k <= 10^9

解法

範囲更新として、遅延セグメント木を検討する。
遅延セグメント木を考えるため、モノイドMと作用素Opの構造、それらの写像、単位元を考える。

まず、モノイドMについて必要そうな構造を考える。
query処理で必要なのはq=0の時で、Σa_iが必要。また、q=4で、iについてのF_i値がそれぞれ個別に必要となる。
ここで、{a_i, F_i}という元を考える。
二項演算●は、和が欲しいので、{a_i, F_i}●{a_j, F_j}={a_i+a_j, F_i+F_j}で考える。
(F_i部分も、結局k倍したものの和が欲しいので、和のk倍から求めるのに和の形にしておく)
単位元は{0, 0}にする。

次に、上記のMを踏まえつつ、作用素Opについて考える。
いま必要なのは「kに置き換える」「kを加える」「kをかける」「k*F_iを加える」の4操作になる。
{a_i, F_i}に対して、「a_iにxをかける」「a_iにF_iのyをかけたものを加える」「a_iにzを加える」という3つを考えると、
「kに置き換える」 <=> (x,y,z) = (0,0,k)
「kを加える」 <=> (x,y,z) = (1,0,k)
「kをかける」 <=> (x,y,z) = (k,0,0)
「k*F_iを加える」 <=> (x,y,z) = (1,k,0)
で表現して、{a_i, F_i}に対して(x,y,z)を作用させると{a_i*x+F_i*y+z, F_i}になるように考えればよいことがわかる。

区間に対する操作で、要素数に応じて変化する部分を考える。
区間の要素を一様にx倍する場合は、要素をまとめあげた区間の構造に対してx倍するのと変わらないが、xを加える場合は、要素数*xが増えるので、考慮する必要がある。
要素数がlenの区間を考えている場合は、{a_i, F_i}に対して(x,y,z)を作用させると{a_i*x+F_i*y+z*len, F_i}になるように考えればよい。

作用素同士は、
{a_i, F_i} ● (a,b,c) ● (p, q, r)<=> {a*a_i + b*F_i + c, F_i} ● (p, q, r)<=> {(a*a_i + b*F_i + c)*p + q*F_i + r, F_i}<=> {a_i, F_i} ● (a*p, b*p+q, c*p+r)
より、 (a,b,c) ● (p, q, r) = (a*p, b*p+q, c*p+r)と計算してあげればよい。

作用素の単位元は、何も作用しないのと同じになる(1,0,0)を考えればよい。

ここまでで、遅延セグメント木を適用でき、十分高速に答えを求められる。
(各計算はちゃんとmodとって計算する)

Tenka1 Programmer Contest 2018 E. Equilateral

問題

HxWのグリッドにコインがいくつか置かれている。
このとき、相異なるコインの3つ組で「その3つのうち、どの2つのコインを取っても、それらの存在する座標の間のマンハッタン距離が一定」であるようなものの個数を求めよ。

制約

• 1 <= W, H <= 300

解法

「マンハッタン距離が一定」というのは、実際に図示してみると、ある点を中心とした正方形を45度回転させたところになる。

他の2点はこの正方形の線上に乗っている必要がある。
適当に2点を定めてみると、該当する点の範囲(赤い領域)は以下のように絞られる。

しかし、単純に2点を選んで3点目を考えてしまうと、3点目がO(1)で求められたとしてもO(W*H * W*H)になってしまい間に合わない。
ここで無駄なところを探してみると、「ある点xを決めた場合、残り2点のうちどちらかは必ずxの45度斜めに存在する」、ということに気付く必要がある。

ある点xに対して、45度斜め方向にある点yがある場合、最後の3点目zは上の図の一番右の図のように赤い範囲の部分となる。
赤い範囲の部分に点が何個あるか？は、前もって累積和を求めておけばO(1)で求められるので、点xを決めるのにO(W*H)、点yを見つけるのにO(W+H)、点zを見つけるのにO(1)、累積和を計算するのにO( (W+H)*(W+H) )で、全体としてO(W*H*(W+H))≒O(N^3)程度で求められる。

実装

上記のアルゴリズムを実装するのに、単純に45度の4方向すべてに対して求めると重複で数え上げてしまうので、その分を引いてあげる必要がある。

解説放送では、盤面全体を90度回転を4回行い、それぞれの回転ごとに、以下の部分をカウントする方法が紹介されていた。

ある点xについて、その右上方向の45度方向にだけ点yを探し、点zの範囲のうち、一番右上の部分だけカウントしない。
もしそのカウントしない部分に点zがあった場合は、時計回りに90度回転したときにカウントされる。
右下の範囲については、180度回転した場合にカウントされ、右上のカウントしないところも270度回転したときにカウントされるので、重複なくカウントできる。(天才)

反省

添え字間違い、範囲外アクセスなどしまくった。
怪しい部分は範囲外アクセスなどしていないかチェックする。

あと、斜めのまま実装したけど、「絶対値を見たら45度回転」から45度回転した状態で処理した方がいろいろミスがなさそう。。。

AGC028 B. Removing Blocks

問題

1～Nの番号が書かれた箱が1列に並べてあり、各箱の重さは整数A_iで与えられる。
この箱を一つずつ取り除いていくことを考える。
ある箱を取り除くときのコストは、その両隣に連続している箱の重さの総和になる。
取り除き方はN!通り考えられるが、そのすべての取り除き方について、N回の取り除くコストの総和の合計を求めよ。

制約

• 1 <= N <= 10^5
• 1 <= A_i <= 10^9

解法

各箱について取り除かれる回数e_iがわかれば「Σ e_i * A_i」で求められる。
制約的にこの計算をO(NlogN)以下の計算量で行う必要がある。

(気付くのが厳しいが、)全事象を考えているので、確率的に考えて期待値を求めることでこのe_iを求める。

ある箱jが取り除かれるとき注目している箱iが連結している確率p_ijが求められれば、その期待値は「N! * Σ_{j=1}^N p_ij」で求められる。
jとiが連結している確率p_ijを考えると、iからjまでの連続した箱のうち、jが最初に選ばれる確率と同じであるので、p_ij = 1 / (abs(i-j)+1)と求められる。

今、MODで計算しているため、p_ijは逆元を計算しておけば整数値になる。
さらに、Σp_ijを考えるとき、p_ijは1/1+1/2+1/3+...のように連続した和になるので、累積和を求めておけばO(1)で求められる。

したがって、e_iがO(N)で求められ、Σe_i * A_iもO(N)で求められるので、全体でO(N)で求められる。

反省

DPや法則性の方向で考えてしまっていたので、確率・期待値の発想がまったく考慮できていなかった。
p_ijの形も解説のようにすぐ導出できなかったので、確率・期待値問題の練習がかなり必要・・・

yukicoder No.743 Segments on a Polygon

問題

M頂点の凸多角形の頂点同士をN本順番に線分で結ぶ。
このとき、頂点は一度線分に使われたら2度は選ばれない。
i番目に結んだ線分の頂点a_iとb_iの情報が与えられるので、追加した線分同士の交点の総数を答えよ。
(もし、ある交点が複数の線分からなる場合は、1つの交点ではなく、各線分同士の交点として数え上げる)

制約

• 1 <= N <= 10^5
• 3 <= M <= 2*10^5
• 0 <= a_i, b_i < M

解法

頂点a_iとb_iを結ぶときは、始点終点ではないので、a_iとb_iを交換してもかまわないことがわかる。以下、a_i < b_iで考える。
重要な性質として、「頂点を結ぶ順番は関係ない」ということに気付く必要がある。

交点ができるケースを考えるために、多角形を直線上にのばして、線分を曲線で表した以下のような図を考える。

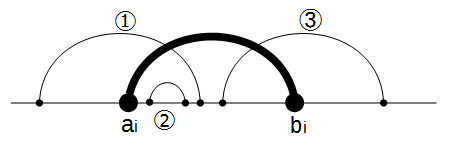
今は、太線の線分を追加する場合を考える。
交点ができるケースは、①と③のケースで、a_iからb_iの間にある頂点に、a_i以下b_i以上の頂点からの線分がある場合になっている。

図の左側付近(①と②のケース)を考える。
左側から太線の交点を作る①(a_j, b_jとする)は、a_jがa_iよりも左側にあり、交点を作らない②(a_k, b_kとする)は、a_kがa_iよりも右側にある。
したがって、「頂点を結ぶ順番は関係ない」性質から、左側から順番に線分を追加していき、すでに結んだ頂点のうち、bにあたる部分がa_iとb_i内に何個あるか？がわかればよい。
これはBITなどでO(logM)で求められる。

図の右側付近(③のケース)を考える。
しかし、③を追加する場合を考えると、これは上記の①のケースに当たるので、太線の追加時には考えなくてよいことがわかる。

したがって、追加する線分のa_iを小さい方から順番に追加していき、追加した線分のb_iをBITなどで記録しつつ、a_j, b_jの線分を追加する場合は、a_jからb_j内に含まれるb_iの個数をカウントしていけばO(N log M)で求められる。

ARC103 E. Tr/ee

問題

各文字は0または1の長さnの文字列sが与えられる。
n頂点の木について考えたとき、

• i文字目が0なら、木からどのように辺を1つ取り除いてもサイズiの連結成分が作れない
• i文字目が1なら、木からある辺を1つ取り除いてサイズiの連結成分を作れる

を満たすような木を実際に1つ構築せよ。
構築できない場合は-1を出力せよ。

制約

• 2 <= n <= 10^5

解法

小さいケースで考えてみると、

• 一番最後の文字が1の場合は構築できない
• リーフの頂点につながる辺を除くと連結成分が1のものが必ずできるので、最初の文字は必ず1でないといけない
• 辺を取り除いてサイズxの連結成分ができたら、対称的にN-xの連結成分ができるので、文字列は最後の文字を除いて対称になっていないといけない

ということがわかる。
以下、上記の条件を満たすような文字列について考える。

今、満たしたい連結成分集合が{1,3,5,...}のような場合を考える。
「1」は、リーフの部分の辺を切ればよい。
「3」は、木の形を考えてみると、以下のようなものになる(赤枠と交差している辺を切ればよい)。

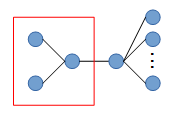
「5」は、上記の形を残しつつ、5個の頂点を入れる必要があるので、以下のように青枠を考えればよい。

もし、「5」ではなく「6」だった場合は、以下のように頂点を増やせばよい。

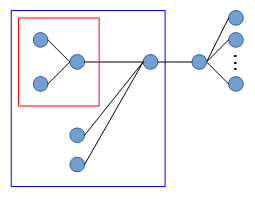
上記のように、与えられた連結成分集合の小さい方から考えて、それまでの形を残しつつ、順次構築していけば目的の木が作れる。

上記の木は、「キャタピラ木」といい、線グラフの各頂点にいくつか頂点を生やしたような木になっている。
Caterpillar tree - Wikipedia

生やした部分はリーフなので、必ず連結成分は1のものができ、線グラフの部分の辺を消すことが題意に相当する。

反省

木の形はある程度限られるので、時間がもう少しあれば、いろいろな木を書いて見ている中でたどり着けたかもしれないけど、、、
「順次構築」的な発想をするようにしていれば効率的にたどり着けたかもしれない。

ARC103 D. Robot Arms

問題

m本の腕とm+1個の関節からなるロボットアームを考える。
腕iの長さはd_i。
関節iは腕iと腕i+1をつないでおり、関節1は原点に置かれ、各関節の角度は上下左右方向に指定できる。

いま、N個の平面上の整数点が与えられる。
すべての整数点にぴったり関節m+1を合わせられるようなロボットアームを返せ。
また、各整数点について、実際にその点に合わせられるような関節の指定値を出力せよ。
できない場合は-1を出力せよ。

制約

• 入力はすべて整数
• 1 <= N <= 1000
• -10^9 <= X_i, Y_i <= 10^9
• 1 <= m <= 40
• 1 <= d_i <= 10^12, d_iは整数

解法

小さいケースで試してみると、(0,1)と(1,1)のように1だけずれた点を同時に満たすロボットアームが構築できないことはすぐわかり、この考えを進めると、座標の(x+yの)偶奇がそろっている場合しかダメなことがわかる。
以下、偶奇がそろっている場合を考える。

整数点の座標は結構大きい値だが、腕の数が40程度のため、うまく長い腕と短い腕を組み合わせる必要がある。
そのような組み合わせとして(構築ゲーでよく出てくる)2冪の長さを考える。

m=1で、腕の長さが{1}の場合、以下のような到達点になる。

m=2で、腕の長さが{1,2}の場合、{1}の時の到達点を上下左右に2ずらしたところになるので、以下のような到達点となる。

したがって、{1,2,4,8,16,...}と2冪の長さで考えると、穴なくひし形範囲内のすべての点にたどり着けるようなロボットアームを構築できる。
上記はx+yが奇数の場合だが、偶数の場合は、{1,1,2,4,8,16,...}のように1を加えたものを考えればよい。

次に、整数点への関節の指定値の構築を考える。
これは、腕の長さが長いものから{2^30, 2^29, ... , 4, 2, 1}のようにしておき、原点からスタートして、上下左右の中で一番目的に近づくように設定するものを選んでいけばよい。

反省

• マンハッタン距離なので、x軸とy軸は独立に考えられそう
• 単純に半分に分けるとm=20程度で10^9を作らないといけないし、mをx軸とy軸でうまく分けたとしてもどっちも10^9程度の時に破たんしそう

みたいな考え方をしてしまって、単純に2冪だけでできる方向の考察ができなかった、、、

yukicoder No.737 PopCount

問題

Nが与えられる。
を求めよ。
(popcount(i)は、iを2進数表記したときの立っているビットの数)

制約

• 1 <= N <= 10^18

解法

法則性がないか見るために、各数字のビットを書き出してみる。

1bit目が1になるものは、{1},{3},{5},{7},{9},...
2bit目が1になるものは、{2,3},{6,7},{10,11},...
3bit目が1になるものは、{4,5,6,7},{12,13,14,15},...

各bit目ごと(上の表の縦方向)に見ると、「塊が等間隔で現れている」という法則性が確認できる。
そこで、「x bit目について、N以下でbitが立っている数字の和」を求める方法を考えれば、それぞれのxで求めたものを足せば答えが得られる。

ということで、「x bit目について、N以下でbitが立っている数字の和」を考える。
最初の塊は、最初の数字が2^{x-1}で、x個続いている。
また、塊は間隔が2^xごとになっており、塊の数は、等差数列より「(N-2^{x-1})/2^x + 1」個ある。
したがって、これらは「等差数列の和の公式 Sn = n / 2 * (2*a + (n-1) * d)」を使えばO(1)で求められる。
また、Nが固まりの途中までの場合は、N+1から塊の最後の数字までの分の和を引いてあげればよい。

ABC110 C. String Transformation

問題

英小文字からなる文字列S, Tがある。
Sに対して、次の操作を0回以上行える。

• 2つの異なる英小文字c1, c2を選び、Sに含まれるすべてのc1をc2に、c2をc1に同時に置換する

操作を行うことでSをTにすることができるか？

制約

• 1 <= Sの長さ <= 2 * 10^5
• Sの長さ = Tの長さ

解法

Sの長さは結構長いが、すべての同じ文字が同時に置換されるので、高々26文字を考えればよい。
題意から素直に「S側の文字aを(T側に対応する)文字xにする」ということを考える。

まず、「S側のある文字aが、文字x, y, ...(2文字以上)にする」ようなS,Tが与えられたら、操作不可能なので、「できない」。
したがって、「S側の文字aを文字x(1文字)にする」ことができる必要がある。

与えられたS, Tから「a -> x」「b -> y」「c -> z」のような文字の変換表が作れたら、素直にチェックすればよい。

S: abcxyz
T: xyzghi

S, Tは、変換表にある文字だけに圧縮できるので上記のようになっているはず。これを左から実際に変換していく。
このとき、「xをxにする」ようなモノはいじる必要がないので、除いておいてよい。

まず、「aをxにする」ことを考え、操作(a,x)をする。
すると、Sは「xbcayz」になり、1文字目が確定する。
置き換えた「文字x」は2文字目以降の操作では使えないので、もしでてくるようなら「できない」。
2文字目以降も同様に繰り返して最後まで変換できるなら、「できる」になる。

解法2

AtCoder Beginner Contest 110 解説放送 - YouTube

SからTにするというのは、Sの文字をTにある文字に対応させるということなので、以下のような(1対1)対応関係を考えて、右側の文字を操作によって入れ替えていくことに相当する。

a -> a
b -> b
c -> c
d -> d
...
z -> z

たとえば、「S側でaだったものをcにしたい」場合は、対応関係の右側でcだったところとswapして、

a -> c
b -> b
c -> a
d -> d
...
z -> z

続けて「S側でcだったものをdにしたい」場合は、

a -> c
b -> b
c -> d
d -> a
...
z -> z

のようにしていることが、操作をしていることに対応している。

上記の操作が問題なくできれば「できる」が、うまくいかないケースを考える。
対応関係の左側と右側それぞれで2種類以上の文字への対応が存在する場合「できない」。
1つ目は、「S側でaだったものをxにしたい」と「S側でaだったものをyにしたい」が発生する場合は「できない」ことがわかる。
2つ目は、「S側でaだったものをxにしたい」と「S側でbだったものをxにしたい」が発生する場合は「できない」。
これらを調べればよい。

AGC027 B. Garbage Collector

問題

数直線上にN個のゴミが落ちており、左からi番目のゴミの位置はx_iにある。
ゴミ箱は位置0にあり、掃除ロボットを動かすことですべてのゴミをゴミ箱に入れたい。

掃除ロボットには以下の制約がある。

• 最初は位置0にいる
• 現在持っているゴミの数をkとすると、距離1あたりの移動には(k+1)^2だけエネルギーがかかる
• ゴミを拾う、または、ゴミを捨てるのにはXのエネルギーを消費する

すべてのゴミを回収するのにかかるエネルギーの最小値を答えよ。

制約

• 1 <= N <= 2 * 10^5
• 0 < x_i <= 10^9
  • x_iは整数
  • x_i < x_{i+1}
• 1 <= X <= 10^9

解法

ロボットの動きを考えてみると、行きは何も回収せず、帰りがけにゴミをいくつか回収して戻ってくるのがエネルギーを抑えられそうというのがわかる。
ただ、どのゴミを回収すればよいかはぱっと見ではわからない。
また、移動エネルギーは持っているゴミの数に依存するので、「あるゴミの回収にかかるエネルギー」は独立に計算できない(そのゴミ以外に同時に回収するゴミがなんなのかが計算には必要)。

そこで、まず、あるk個のゴミを考え、それを回収するのにかかるエネルギーがどのように計算されるか考える。
拾う・捨てるのエネルギーは、各ゴミを拾う「k * X」と捨てる「X」の和「k * X + X」になっている。
今、ゴミの位置が左から「a,b,c,d」だとすると、移動にかかるエネルギーを考えると、
行き：1 * d
帰り：4 * (d-c) + 9 * (c-b) + 16 * (b-a) + 25 * a
なので、これを足して整理すると、
5 * d + 5 * c + 7 * b + 9 * a
となり、「ゴミ集合の遠い方のゴミから位置に5,5,7,9,11,13,...をかけたもの」になっていることがわかる。
したがって、N個のゴミをいくつかの集合に分解して考えるとき、その集合の移動エネルギーは上記の方法で求められる。

N個のゴミをm個の集合に分けることを考えると、上の「遠い方のゴミから位置に5,5,7,9,11,13,...をかけたもの」がその集合の移動にかかるエネルギーになることから、できるだけ遠くの位置にあるゴミに小さな係数がかかるように集合を定義してあげたほうがエネルギーが小さくなり良いということがわかる。
これは、例えば、m=3で、ゴミの位置が左から「a,b,c,d,e,f,g,h,i,j,k,l」のような場合だと、(m=)3つの各集合は、(遠い方から)

• l, i, f, c
• k, h, e, b
• j,g,d,a

のように選んであげれば、

• 5 * l + 5 * i + 7 * f + 9 * c
• 5 * k + 5 * h + 7 * e + 9 * b
• 5 * j + 5 * g + 7 * d + 9 * a

がそれぞれの集合での移動にかかるエネルギーになっている。
これは、位置が遠い方からm個ごとのかたまりを作って、遠い塊から5,5,7,9,11,13,...をかけている。
m個の塊の合計は累積和を使えばO(1)で求められ、5,5,7,9,11,13,...をかける行為はceil(N/m)回の掛け算になっている。
また、拾う・捨てるのエネルギーは、各ゴミを拾う「N * X」と捨てる「m * X」の和「N * X + m * X」になっている。

mを1〜Nまでループをまわすことを考えると、各集合のエネルギーを求める部分でceil(N/m)回の掛け算を行うことになるが、「O(Σ_{1 <= i <= N} N/i) = O(NlogN)」である性質を考えると、2重ループを回しても全体でO(NlogN)の計算量になる。
桁あふれがあり得るので溢れないように注意。

反省

本番では、ゴミの連続区間でみて端からDPするのを考えてしまった(嘘解法)。
コードに間違いがなさそうでアルゴリズムに問題があると気づくまで何回かWAを投げてしまったし、歯抜けな回収が最適な場合があると気づいて次に考えたのが、各辺での通り方についてだったので、全然解法にたどり着けなかった、、、
「辺(距離)に対して条件があっても式を整理すると点(位置)に対して計算することができる」は覚えておく。

ARC008 D. タコヤキオイシクナール

問題

ベルトコンベアにN個のトンネルが一直線に並んでいる。
トンネルには実数のペア(a,b)が書かれており、おいしさrのタコヤキがそのトンネルを通ると、おいしさがa*r+bに変化する。
最初はトンネルの実数のペアはすべて(1,0)になっているが、M回トンネルの一つを選びその実数のペアの値を変更する。
各変更によって、おいしさ1のタコヤキがすべてのトンネルを通った後においしさがどうなるか知りたい。おいしさの最小値と最大値を求めよ。

制約

• 1 <= N <= 10^12
• 0 <= M <= 100,000
• -1.0 <= 変更後のa,b <= 1.0

解法

セグメント木はモノイド(二項演算と単位元)に適用でき、

• 二項演算(2つのトンネルを連結させる)
  • 「x -> (a,b) -> (c,d) -> ?」は「x -> (a*c,b*c+d) -> ?」にできる
• 単位元
  • (a,b)=(1,0)

と考えればよい。

非可換な二項演算なので、以下の「Non-commutative combiner functions」を参考にセグメント木を作ればよい。
Efficient and easy segment trees - Codeforces

変更が行われた後は、すべてのトンネルを通った後の結果を知りたいので、セグメント木のルートノードの情報を使えば求められる。

Nが大きいが、Mが小さいので、あらかじめ与えられる変更情報に含まれないものは無視(座標圧縮)しておけばよい。

SoundHound Inc. Programming Contest 2018 -Masters Tournament- Qual E. + Graph

問題

辺に正の重みがある連結なグラフが与えられる。
いま、以下の条件を満たす頂点に正の整数を書き込みたい。

• どの辺も、両端の頂点の整数の和が辺の重みに等しい

条件を満たす正の整数の書き方は何通りあるか？

制約

• 2 <= 頂点数 <= 10^5
• 1 <= 辺の数 <= 10^5
• 2 <= 辺の重み <= 10^9

解放

頂点に書き込める整数の制約がわからないので、まず、適当に1頂点を選びそこをxと書き込む。
すると、その頂点から辺(重みはsとする)を通って行ける頂点の整数はs-xに決まる。
このように多項式「ax+b」を伝搬していくことを考えると、グラフは連結なのですべての頂点に1つ以上多項式が割りあたる。
答えは、最終的にすべての頂点の条件についてxの下界・上界を見てあげれば、何通りxの書き方があるかがわかる。

頂点に多項式が1つ割りあてられているときは、その多項式が正の整数であること「ax+b > 0」を満たせばいいので、「x > -b/a」を考えれば良い。
頂点に多項式が2つ割りあてられているときは、その2つは同じ値にならなければ矛盾してしまうので、ax+b=cx+dからx = (d-b)/(a-c)でなければならず、「そのxが正の整数であること」と「そのxをax+b、cx+dに入れてもどちらも正の整数になること」を考えれば良い。
(a-c=0や(d-b)/(a-c)が割り切れない場合は解がないので0を返す)
頂点に多項式が3つ以上割りあてられているときは、2つ割りあてられているときと同様にすべての多項式が同じ値にならなければいけないが、3つ以上の異なる多項式だとxは解がないので0を返せば良い。
よって、ループなどで無数に多項式が割りあたるケースは、伝搬中に多項式が3つ以上割りあたる頂点にたどり着いた時点で伝搬を中止し0を返せば、制限時間に間に合う。

ARC101 D. Median of Medians

問題

長さNの数列aが与えられる。
数列aのすべての連続部分列について中央値を並べ、新たに数列mを作る。
この数列mの中央値を求めよ。
ただし、偶数個の数列の中央値は、ソートし小さい方からfloor(M/2)+1番目の要素とする。( (10, 20, 30, 40)の場合、中央値は30)

制約

• 1 <= N <= 10^5
• 1 <= a_i <= 10^9
• a_iは整数

解法

求めるのは、数列mにおける中央値だが、数列mの要素数はN*(N+1)/2個もあるため、線形解法は通らない。
そこで、これよりも高速な二分探索で求めることを考える。

二分探索で中央値を求めることを考えると、「ある値X以上の数列mの要素数」がわかれば、その要素数が数列mの要素の半分を超えるところを求めればよい、ことがわかる。

次に、「ある値X以上の数列mの要素数」、すなわち、「数列aでの連続部分列で中央値がX以上の個数」を高速で求めたい。
ある連続部分列で中央値がX以上になるのは、連続部分列内の要素について「X未満の要素数 <= X以上の要素数」になる場合である。
これは以下のように考えることでO(NlogN)で求めることができる。

数列aにおいて、「X未満の要素」を-1、「X以上の要素」を+1とした数列bを考える。
数列a=(10,30,20)でX=20なら、数列b=(-1,+1,+1)となる。
求めたい「X未満の要素数 <= X以上の要素数となっている連続部分列の個数」は、数列bにおいて「総和が0以上になっている連続部分列の個数」になる。
連続部分列の総和が0以上かどうかは、累積和(最初に0を加えたN+1要素)を取って、lとrの位置での累積和を見て、「位置lでの累積和<=位置rでの累積和」になっていればよい。
ここで、累積和の値である2点の大小関係が異なる個数というのは「転倒数」であり、BITなどでO(NlogN)で求められるので、連続部分列の個数から転倒数を引けば、求めたい連続部分列の個数が求まる。

AGC020 C. Median Sum

問題

N個の整数A_iが与えられる。
空でない部分列のそれぞれの和をすべて考える。これは2^N-1個存在していて、奇数個ある。
この和を昇順で並べたものの中央値を求めよ。

制約

• 1 <= N <= 2000
• 1 <= A_i <= 2000

解法

実は「選んだ部分列」と「選ばなかった部分列」が対応関係になっている。
全部の和をSとし、選んだ部分列の和をaとすると、選ばなかった部分列はS-aになるが、部分列の和をソートしたとき、aが中央より左になるなら、S-aは中央より右になるような対応になる(逆も)。

この対応関係を考えると、中央値は「S/2以上で一番小さい値」であることがわかる(Sが奇数の場合は、S/2を超える最小の整数で考えればよい)。

これを求めるには、値が作れるか見ればいいので、「dp[s] := 部分列の和がsのものが作れるか否か(0/1)」を作って、上記の条件を満たす値を探せばよい。
dpは最大4,000,000で、bitsetを使って以下のようにシフト演算すると高速に計算できる。

dp[0] = 1;
rep(i,N){
  dp |= dp << A[i];
}

ARC102 D. All Your Paths are Different Lengths

問題

整数Lが与えられるので、以下の条件を満たす有向グラフを返せ。

• 多重辺が含まれていてよい
• 頂点数Nは20以下で、すべての頂点は相違な1～Nの番号が付けられている
• 辺数Mは60以下で、すべての辺には0～10^6以下の整数の長さがつけられている
• 辺は、頂点番号が小さいものから大きいものへとのみ張られている
• 頂点1から頂点Nへの異なるパスがちょうどL個、かつ、それらパスの長さが0～L-1までの相違な整数になっている
  • パスの長さとは、パス上の辺の長さの総和
  • 異なるパスとは、パス上の辺の集合が異なること

制約

• 2 <= L <= 10^6

解法

まず、「パスの数がちょうどL個」の方から考える。
頂点数が20程度で10^6個のパスを作る必要があり、2乗をうまく駆使してグラフを作る必要がある。
多重辺が許されない場合は、すべての頂点から辺が張れる頂点へ辺を伸ばすと各頂点へのパスが2乗になってくれるが、辺の数が60本を超えてしまう。
多重辺を許される場合、頂点間の辺の本数を1本から2本にすると、そこまでのパスを2倍にすることができる。
したがって、単純にN頂点を番号順に並べて、頂点iから頂点i+1へ辺を2本張れば、各頂点へのパス数が2乗になって、Lを2進数で表記したとき1となるものに対応する頂点から最後の頂点へ辺を張ればパスの数をちょうどL個にできる。

ただし、Nの制約が20以下で、頂点数がかなりぎりぎりのため、2乗の頂点とは別に最後の頂点を用意しようとすると足りなくなってしまうので注意。
イメージとしては以下のような感じ(頂点1～4まででパスを作って、2進表現に該当する部分を長さW,X,Y,Zの辺の有無で調整)だけど、

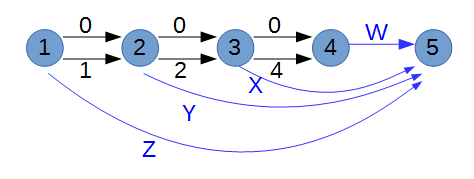
頂点数を節約するのに以下のようにして頂点を減らして考えた。。。
(長さWの辺は自己ループになるので削除し、代わりに一つ前の頂点から伸びている辺(長さ0と長さ4の辺)の長さにWを加算して扱う)

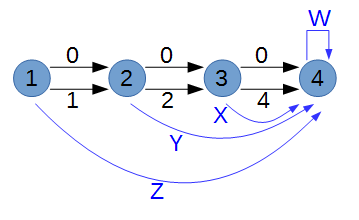
次に「パスの長さが0～L-1までの相違な整数になる」を考える。
今、辺は「隣り合う頂点に2本」と「各頂点から最後の頂点へ1本あるかないか」の状態になっている。
パスがL個で0～L-1までちょうど使い切る必要があるため、きれいに割り当てないといけない。

ここで、規則性を持たせるため、隣り合う頂点間の2本の辺に「長さ0の辺」と「長さ2^(i-1)の辺」を貼ることを考える。
すると、各頂点までのパスの長さは「0～(2^(i-1))-1の長さがすべて含まれる」。
あとは、「各頂点から最後の頂点への辺(図でいうところのW, X, Y, Z)」の部分で、0～L-1に被らないように割当たるように辺の長さ(W, X, Y, Z)を決めてあげればぴったり割り当てられる。
(後ろから決めていく方法だと、Lからパスの数を引きつつW, X, Y, Zの順番で値を決めていく。Zは必ず0)

解法2

解説放送での方法。
AtCoder Regular Contest 102/ Beginner Contest 108 解説放送 - YouTube
L=Xがわかっているとき、「L=2Xを作る方法」と「L=X+1を作る方法」が決まれば、それを繰り返すことで構成することができる。

最小のL=2の時は、頂点数が2つで、頂点1から頂点2への長さが0の辺と1の辺であることが一意に決まる。

「L=2Xを作る方法」は、新しく頂点を追加し、L=Xでのグラフの最後の頂点から新しく追加した頂点へ辺を2本追加してあげればパスの数を2倍にできる。また、L=Xでのグラフの長さをすべて2倍にし、追加した辺の長さは0と1とすると作れる。
(追加した2本の辺の長さは0とXとするでもよい？)

「L=X+1を作る方法」は、一番最初の頂点から最後の頂点に辺を増やせばパスの数は作れる。辺の長さはXとすればよい。

反省

多重辺なしの2乗のイメージからスタートしてしまって、多重辺をうまく使えず、「パスの数がちょうどL個」の構成でハマってしまった。
基本的に、制約はすべて使い切って考える。