ARC008 D. タコヤキオイシクナール
問題
ベルトコンベアにN個のトンネルが一直線に並んでいる。
トンネルには実数のペア(a,b)が書かれており、おいしさrのタコヤキがそのトンネルを通ると、おいしさがa*r+bに変化する。
最初はトンネルの実数のペアはすべて(1,0)になっているが、M回トンネルの一つを選びその実数のペアの値を変更する。
各変更によって、おいしさ1のタコヤキがすべてのトンネルを通った後においしさがどうなるか知りたい。おいしさの最小値と最大値を求めよ。
制約
- 1 <= N <= 10^12
- 0 <= M <= 100,000
- -1.0 <= 変更後のa,b <= 1.0
解法
セグメント木はモノイド(二項演算と単位元)に適用でき、
- 二項演算(2つのトンネルを連結させる)
- 「x -> (a,b) -> (c,d) -> ?」は「x -> (a*c,b*c+d) -> ?」にできる
- 単位元
- (a,b)=(1,0)
と考えればよい。
非可換な二項演算なので、以下の「Non-commutative combiner functions」を参考にセグメント木を作ればよい。
Efficient and easy segment trees - Codeforces
変更が行われた後は、すべてのトンネルを通った後の結果を知りたいので、セグメント木のルートノードの情報を使えば求められる。
Nが大きいが、Mが小さいので、あらかじめ与えられる変更情報に含まれないものは無視(座標圧縮)しておけばよい。
SoundHound Inc. Programming Contest 2018 -Masters Tournament- Qual E. + Graph
問題
辺に正の重みがある連結なグラフが与えられる。
いま、以下の条件を満たす頂点に正の整数を書き込みたい。
- どの辺も、両端の頂点の整数の和が辺の重みに等しい
条件を満たす正の整数の書き方は何通りあるか?
制約
- 2 <= 頂点数 <= 10^5
- 1 <= 辺の数 <= 10^5
- 2 <= 辺の重み <= 10^9
解放
頂点に書き込める整数の制約がわからないので、まず、適当に1頂点を選びそこをxと書き込む。
すると、その頂点から辺(重みはsとする)を通って行ける頂点の整数はs-xに決まる。
このように多項式「ax+b」を伝搬していくことを考えると、グラフは連結なのですべての頂点に1つ以上多項式が割りあたる。
答えは、最終的にすべての頂点の条件についてxの下界・上界を見てあげれば、何通りxの書き方があるかがわかる。
頂点に多項式が1つ割りあてられているときは、その多項式が正の整数であること「ax+b > 0」を満たせばいいので、「x > -b/a」を考えれば良い。
頂点に多項式が2つ割りあてられているときは、その2つは同じ値にならなければ矛盾してしまうので、ax+b=cx+dからx = (d-b)/(a-c)でなければならず、「そのxが正の整数であること」と「そのxをax+b、cx+dに入れてもどちらも正の整数になること」を考えれば良い。
(a-c=0や(d-b)/(a-c)が割り切れない場合は解がないので0を返す)
頂点に多項式が3つ以上割りあてられているときは、2つ割りあてられているときと同様にすべての多項式が同じ値にならなければいけないが、3つ以上の異なる多項式だとxは解がないので0を返せば良い。
よって、ループなどで無数に多項式が割りあたるケースは、伝搬中に多項式が3つ以上割りあたる頂点にたどり着いた時点で伝搬を中止し0を返せば、制限時間に間に合う。
ARC101 D. Median of Medians
問題
長さNの数列aが与えられる。
数列aのすべての連続部分列について中央値を並べ、新たに数列mを作る。
この数列mの中央値を求めよ。
ただし、偶数個の数列の中央値は、ソートし小さい方からfloor(M/2)+1番目の要素とする。( (10, 20, 30, 40)の場合、中央値は30)
制約
- 1 <= N <= 10^5
- 1 <= a_i <= 10^9
- a_iは整数
解法
求めるのは、数列mにおける中央値だが、数列mの要素数はN*(N+1)/2個もあるため、線形解法は通らない。
そこで、これよりも高速な二分探索で求めることを考える。
二分探索で中央値を求めることを考えると、「ある値X以上の数列mの要素数」がわかれば、その要素数が数列mの要素の半分を超えるところを求めればよい、ことがわかる。
次に、「ある値X以上の数列mの要素数」、すなわち、「数列aでの連続部分列で中央値がX以上の個数」を高速で求めたい。
ある連続部分列で中央値がX以上になるのは、連続部分列内の要素について「X未満の要素数 <= X以上の要素数」になる場合である。
これは以下のように考えることでO(NlogN)で求めることができる。
数列aにおいて、「X未満の要素」を-1、「X以上の要素」を+1とした数列bを考える。
数列a=(10,30,20)でX=20なら、数列b=(-1,+1,+1)となる。
求めたい「X未満の要素数 <= X以上の要素数となっている連続部分列の個数」は、数列bにおいて「総和が0以上になっている連続部分列の個数」になる。
連続部分列の総和が0以上かどうかは、累積和(最初に0を加えたN+1要素)を取って、lとrの位置での累積和を見て、「位置lでの累積和<=位置rでの累積和」になっていればよい。
ここで、累積和の値である2点の大小関係が異なる個数というのは「転倒数」であり、BITなどでO(NlogN)で求められるので、連続部分列の個数から転倒数を引けば、求めたい連続部分列の個数が求まる。
AGC020 C. Median Sum
問題
N個の整数A_iが与えられる。
空でない部分列のそれぞれの和をすべて考える。これは2^N-1個存在していて、奇数個ある。
この和を昇順で並べたものの中央値を求めよ。
制約
- 1 <= N <= 2000
- 1 <= A_i <= 2000
解法
実は「選んだ部分列」と「選ばなかった部分列」が対応関係になっている。
全部の和をSとし、選んだ部分列の和をaとすると、選ばなかった部分列はS-aになるが、部分列の和をソートしたとき、aが中央より左になるなら、S-aは中央より右になるような対応になる(逆も)。
この対応関係を考えると、中央値は「S/2以上で一番小さい値」であることがわかる(Sが奇数の場合は、S/2を超える最小の整数で考えればよい)。
これを求めるには、値が作れるか見ればいいので、「dp[s] := 部分列の和がsのものが作れるか否か(0/1)」を作って、上記の条件を満たす値を探せばよい。
dpは最大4,000,000で、bitsetを使って以下のようにシフト演算すると高速に計算できる。
dp[0] = 1;
rep(i,N){
dp |= dp << A[i];
}
ARC102 D. All Your Paths are Different Lengths
問題
整数Lが与えられるので、以下の条件を満たす有向グラフを返せ。
- 多重辺が含まれていてよい
- 頂点数Nは20以下で、すべての頂点は相違な1~Nの番号が付けられている
- 辺数Mは60以下で、すべての辺には0~10^6以下の整数の長さがつけられている
- 辺は、頂点番号が小さいものから大きいものへとのみ張られている
- 頂点1から頂点Nへの異なるパスがちょうどL個、かつ、それらパスの長さが0~L-1までの相違な整数になっている
- パスの長さとは、パス上の辺の長さの総和
- 異なるパスとは、パス上の辺の集合が異なること
制約
- 2 <= L <= 10^6
解法
まず、「パスの数がちょうどL個」の方から考える。
頂点数が20程度で10^6個のパスを作る必要があり、2乗をうまく駆使してグラフを作る必要がある。
多重辺が許されない場合は、すべての頂点から辺が張れる頂点へ辺を伸ばすと各頂点へのパスが2乗になってくれるが、辺の数が60本を超えてしまう。
多重辺を許される場合、頂点間の辺の本数を1本から2本にすると、そこまでのパスを2倍にすることができる。
したがって、単純にN頂点を番号順に並べて、頂点iから頂点i+1へ辺を2本張れば、各頂点へのパス数が2乗になって、Lを2進数で表記したとき1となるものに対応する頂点から最後の頂点へ辺を張ればパスの数をちょうどL個にできる。
ただし、Nの制約が20以下で、頂点数がかなりぎりぎりのため、2乗の頂点とは別に最後の頂点を用意しようとすると足りなくなってしまうので注意。
イメージとしては以下のような感じ(頂点1~4まででパスを作って、2進表現に該当する部分を長さW,X,Y,Zの辺の有無で調整)だけど、
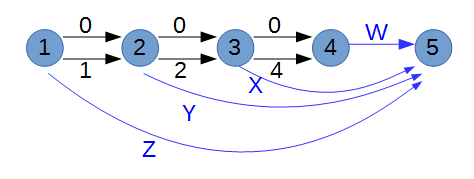
頂点数を節約するのに以下のようにして頂点を減らして考えた。。。
(長さWの辺は自己ループになるので削除し、代わりに一つ前の頂点から伸びている辺(長さ0と長さ4の辺)の長さにWを加算して扱う)
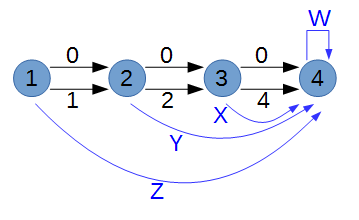
次に「パスの長さが0~L-1までの相違な整数になる」を考える。
今、辺は「隣り合う頂点に2本」と「各頂点から最後の頂点へ1本あるかないか」の状態になっている。
パスがL個で0~L-1までちょうど使い切る必要があるため、きれいに割り当てないといけない。
ここで、規則性を持たせるため、隣り合う頂点間の2本の辺に「長さ0の辺」と「長さ2^(i-1)の辺」を貼ることを考える。
すると、各頂点までのパスの長さは「0~(2^(i-1))-1の長さがすべて含まれる」。
あとは、「各頂点から最後の頂点への辺(図でいうところのW, X, Y, Z)」の部分で、0~L-1に被らないように割当たるように辺の長さ(W, X, Y, Z)を決めてあげればぴったり割り当てられる。
(後ろから決めていく方法だと、Lからパスの数を引きつつW, X, Y, Zの順番で値を決めていく。Zは必ず0)
解法2
解説放送での方法。
AtCoder Regular Contest 102/ Beginner Contest 108 解説放送 - YouTube
L=Xがわかっているとき、「L=2Xを作る方法」と「L=X+1を作る方法」が決まれば、それを繰り返すことで構成することができる。
最小のL=2の時は、頂点数が2つで、頂点1から頂点2への長さが0の辺と1の辺であることが一意に決まる。
「L=2Xを作る方法」は、新しく頂点を追加し、L=Xでのグラフの最後の頂点から新しく追加した頂点へ辺を2本追加してあげればパスの数を2倍にできる。また、L=Xでのグラフの長さをすべて2倍にし、追加した辺の長さは0と1とすると作れる。
(追加した2本の辺の長さは0とXとするでもよい?)
「L=X+1を作る方法」は、一番最初の頂点から最後の頂点に辺を増やせばパスの数は作れる。辺の長さはXとすればよい。
反省
多重辺なしの2乗のイメージからスタートしてしまって、多重辺をうまく使えず、「パスの数がちょうどL個」の構成でハマってしまった。
基本的に、制約はすべて使い切って考える。
ARC102 C. Triangular Relationship
問題
整数N, Kが与えられ、N以下の正の整数の組(a, b, c)を考える。
a+b, b+c, c+aがKの倍数であるような(順番を考慮する)組の個数を答えよ。
制約
- 1 <= N, K <= 2*10^5
解法
2つの整数a, bをループで回してcの候補数を列挙するような方法だとO(N^2)かかってしまい間に合わない。
まず、「Kの倍数」をそのまま扱うのは大変なので、mod Kで考える。
そうすると、「Kの倍数である」<=>「mod Kで0になる」になる。
そこで、mod Kの世界で考え、(a mod K, b mod K, c mod K)の組み合わせを考えると、2つとって足したら0になる必要があるため、実は以下の場合しかない。
- 0を足す場合:(0, 0, 0)
- 0でないものを足す場合:(K/2, K/2, K/2) (ただし、K/2が割り切れること)
したがって、Kが奇数の時は(0, 0, 0)のパターンだけで、「1~Nまででmod Kが0になる個数」が各a,b,cの位置にあり得るので、個数を3乗したものが答え。
Kが偶数の時は、(0, 0, 0)のパターンと(K/2, K/2, K/2)のパターンがあり、同様にそれぞれ個数を3乗したものを足したものが答えになる。
Mujin Programming Challenge 2018 E. 迷路
問題
N*Mのマス目があり、各マスには障害物がある場合がある。
時刻0にスタート地点からスタートし、できるだけ短い時間でゴール地点に移動したい。
各時刻では、「1秒かけて隣接マスに移動する」か、「移動せずにマスに待機する」ことができる。
しかし、各時刻で移動できる方向が1方向にのみ限られており、どの方向に移動できるかは文字列Dで与えられ、時刻tの場合はt mod |D|番目の文字が移動できる方向を示す。
ゴールまでの最短時間を求めよ。
制約
- 2 <= N, M <= 1000
- 1 <= |D| <= 100000
解法
ある地点にいる場合、方向Aの隣接マスに移動するためには、「ぐるっと回って移動する」か、「その場で待つ」ことができる。
その場で待つ場合、移動したい方向の文字になるまで待つ必要がある。
この待ち時間をwait(t, angle)で求められたとすると、結局、「その地点にたどり着く最短時間」がわかっている場合、隣接マスへの移動は「その最短時間+wait(t, angle) + 1」(最後の+1は移動時間)で移動できるので、これでダイクストラすればよい。
wait(t, angle)は単純に計算するとO(|D|)かかってしまうが、前処理として、Dを2つつなげた文字列を後ろからなめて待ち時間をO(1)で求められるようにすれば、全体の計算量はダイクストラの計算量だけになる。
ARC099 D. Snuke Numbers
問題
整数nについて、nを十進数で表したときの各桁の和をS(n)とする。
正の整数nで、nより大きいすべての正の整数mに対してn/S(n) <= m/S(m)が成り立つものをすぬけ数と呼ぶ。
整数Kが与えられたとき、すぬけ数を小さい方からK個列挙せよ。
制約
- 1 <= K
- K番目のすぬけ数は10^15以下
解法
「ある整数xについて、それより大きい整数yでy/S(y)が一番小さいものを求める関数f(x)」を考え、順次適用していくことを考える。
f(x)のアルゴリズムを考える。
まず、xより大きいyはx+1以上の整数で、これを全探索するのは無理なので、探索範囲を減らすことを考えたい。
桁数がkの整数yを考えたとき、k桁の整数のうち、S(n)が最大となるのは、999...999のように9がk個ならんだものになる。
桁数がk+1の整数がこの999...999よりn/S(n)が大きくならなければ、「k桁の整数だけ考えればよい」ということがわかる。
例えば、k=3の場合を考えると、999は、S(n)=27なので、k+1=4桁の整数を考えた場合にS(n)が27以上の整数になっていなければ分子は大きくなるのでn/S(n)は小さくならない。
しかし、4桁の整数で、nをあまり大きくせずにS(n)が27以上整数を考えると、
S(n)=27→一番小さい4桁のnは1899
S(n)=28→一番小さい4桁のnは1999
S(n)=29→一番小さい4桁のnは2999
S(n)=30→一番小さい4桁のnは3999
S(n)=31→一番小さい4桁のnは4999
S(n)=32→一番小さい4桁のnは5999
S(n)=33→一番小さい4桁のnは6999
S(n)=34→一番小さい4桁のnは7999
S(n)=35→一番小さい4桁のnは8999
S(n)=36→一番小さい4桁のnは9999
となっており、nの増え方とS(n)の増え方的に、k+1桁以上のn/S(n)はk桁の9が並んだものより大きいn/S(n)になってしまう。
したがって、k桁のものだけを考えればよい。
とはいえ、すぬけ数は10^15まであるので、15桁程度の探索をそのままするのはまだ無理。
f(x)の候補となる整数をさらに候補を絞りたい。
候補となる整数として、y=12534のような整数を考えると、これはまだyより大きいものでy/S(y)を小さくできるものが考えられて、12539のようにちょっと大きくすることで、S(y)を14から19に増やせてy/S(y)を改善できてしまう。
y=12534より大きいものとして、1桁目を大きくする12535,12536,...12539と、2桁目を大きくする1254x,1255x,...,1259x、3桁目を大きくする126xx,127xx,...・・・と考えられる。
xの部分を任意の整数で考えてみると、1254xはxが9じゃない場合は12539の方がS(y)が小さいため、改善しないことがわかる。
同様に考える3桁目4桁目・・・と、xの部分は9じゃないとそれより改善するものが存在してしまうためxの部分は9だけ考えればよい。
したがって、考えるべきは、1桁目を大きくする場合、2桁目を大きくする場合(ただし、1桁目は9)、3桁目を大きくする場合(ただし1桁目と2桁目は9)、・・・という感じで、桁数*10程度の候補がy/S(y)を小さくする可能性があるので、探索すればよい。
1→f(1)→f(f(1))→・・・と繰り返せばよく、f(x)の計算量は、O(xの桁数*10)程度なので、十分高速に求めていける。
(嘘)解法
理論保証がないアプローチだが、実験して探索範囲を減らして解を探す方法でも通ってしまう。
mは∞まであるが、ある程度の数値で打ち切って実験してみると、xxx99999のような感じになっていることが確認できる。
桁数を増やして、上位3~4桁分を任意の数として後ろに9を並べた数字を考えると、すぬけ数の候補と考えられるので、列挙して、実際にそれらの数値だけ比較して条件を満たすものを返す。
TCO18 MM R2 CrystalLighting
概要
レートのわりに順位がよくて、目標の1つの「1pt以上ゲット(できればTシャツ)」を達成できた:D
最終順位は41位(127人参加)でした。
問題
HxWのセル上にクリスタルまたは障害物が置かれており、各クリスタルには、光らせたい色(原色:青/黄/赤、二次色:緑/紫/橙の6色)が与えられる。
今、空のセルに以下のオブジェクトを置くことができる
- 上下左右にビームが伸びるライト(色は原色の青、黄、赤の3色のみ)
- ビームを反射するミラー(ただし、斜めに置き、ビームを90度回転させる)
- 障害物
二次色クリスタルを光らせるには、2種類のライトのビームで光らされていなければいけない。
スコアを、「(光っているクリスタルについて、色が、正しく原色で光っている場合+20、正しく二次色で光っている場合+30、違う色で光っている場合-10としたときの合計値) - (各オブジェクトを置くコスト)」としたとき、これを最大化せよ。
最終的に提出したアプローチ
- 焼きなまし
- 近傍は、ランダムにセルを選んで、それが空マスなら「85%でライトを置く、5%ずつでミラーまたは障害物を置く」、オブジェクトを置いているマスなら「4近傍1マスに移動」または「そのオブジェクトを消す」
- 評価関数は、前半を二次色が1色には当たっている場合-3にしたもの、後半はスコア通り
- あるマスの4近傍を探索する部分は、探索も更新もO(N)だけど、ちょっとだけキャッシュに残すようにしてみた
- 初期値として、二次色のクリスタルだったらその1マスとなりの4近傍にライトおけたらおいておいたもの、にしておいた
振り返り
今回は方針とか方向性は良かった感じで、1週間の割にはいろいろ入れられた気もする。
方針
単純にスコア計算の差分ができそうなので、焼きなましは有効そうということで、ここのところまでの焼きなましの反省を活かそうと焼きなまし方針にした。
直前にやってたyukicoderマラソンで「変化量の小さい近傍が作れれば、探索空間がなめらかになって探索しやすい」ということを見ていたので、そこら辺を意識。
近傍
最初は単純に「置く」「取り除く」でやっていたけど、これだと「スコア高い→低い→高い」みたいな感じで滑らかじゃないので、それ以外を考えた。
「クリスタルを照らすライトの位置や色をシャッフルする」とか「近くにランダムに移動」とか試してみたけど、初期実装だとスコアがあまり上がらず、結局「隣接4マスどれかに移動」だけを追加した。
高速化
重いところは「あるマスposの方向kに進んだときにぶつかるマスの位置」を求めるところで、最初、set使ってO(logN)な探索がいいかなと思って書いてみたけど、単純にマスをたどるO(N)な方が速くて、O(1)はバグりそうだったので後回しにしてたら結局最後まで手を付けられなかった。
同じマスに結構アクセスしがちなのでキャッシュ的なモノを用意してみたけど付け焼き刃ぐらいだった。
二次色の「0→-10→30」の不連続性
二次色の30点はおいしいのでできるだけおさえておきたかったので、いくつか工夫を考えて入れた。
近傍として「2つ同時置き」とか試してみたけど、試したときはあまりスコア的な効果が見られなかった。。。
回転数が少なかったので、初期状態として「30点をおさえられるならその4近傍にライトを先に置く」をいれておいた。
最初の方は二次色の1色ライトで光っている場合-10点なのを緩和するために、時間の前半分の時はスコアを-3点ぐらいにして、後ろ半分は通常スコアで計算した。
Round1の反省
TCO18 MM R1 RoadsAndJunctions - phyllo’s algorithm note
Round1の反省で、「コードの書き方や管理方法」を工夫する予定だったけど、結局雑に書きすぎてしまった。
インクリメンタルに実装を追加したり消したりするせいで、どんどん継ぎ接ぎになるし、めんどくさがって関数を長くして書き直すつもりをそのままにしたりとひどかった。。。
高速化も、十分できていなかった。
可視化も、結局なにも行わず、公式Testerだけだった。(焼きなましのデバッグに文字列で出力はしたぐらい)
引き続き反省orz。
反省
フォーラムや感想戦見てて得られるものが多かったのでまとめとく。
TCO18 MM R2 - Togetter
TopCoderでプログラムしてみた 第2394回 (TCO 18 Marathon Match Round 2 直後放送) - YouTube
TopCoder Forums
近傍
「ライトの移動」のところは、「ビームライン上に移動」が無駄なく変化量が小さい良い近傍だったもよう。
ランタンの追加・削除は光線4方向分スコアが変化する。ランダムワープなら8本分。
— hakomo (@hakomof) June 15, 2018
でも光線のパス上の移動なら水平に照らすモノは変わらず、変化するのは2本だけ。これがスコア変化量/近傍が小さいということであり、探索空間がなだらかになり、探索量が増える。 pic.twitter.com/ytjmdXtiFA
hakomoさんの考え方の方が汎用的で良いのだけど
— hoshi524 (@hoshi524) June 15, 2018
ランタンの移動は、ランタンを置く理由がいずれかの方向のクリスタルを充足させることで、それを維持しつつ変えたいから移動先は光線上だった
仮にランダムワープが有効なら、設置・削除という近傍でほぼ等価な効果が得られるからランダムワープではない https://t.co/CQfQYVZD2a
採用してた「ライトの1マス移動」は一応変化量を小さい移動を含んでいたけど、不十分だったかも。
また、ビームライン上にランダム移動ではなく、探索して一番いい位置に移動、とか近傍の候補にすら入れられてなかった、、、
ここらへん、適当に近傍案を考えてみて変化量の小さそうなものを使う、としてしまったけど、考察から導出できるようにしたい。
高速化
焼きなましのループ回数は1000万ぐらいを目標にしてたけど、上位陣は1億回ぐらい回っていたらしく、文字通り桁が違ってた。
高速化で重要そうだったのは、診断人さんの放送で議論されている、
- 4近傍の探索をO(1)にする (更新はO(N)でもよい)
- 焼きなましの更新の仕方を「状態更新→スコア計算→悪化なら状態戻す」ではなく「スコア計算→良化なら状態更新」にする
ところだった模様。
「4近傍の探索O(1)」は、考えてたけどバグりそうで後回しにして結局手を付けられなかった。
けど、ミラーを考慮した厳密なO(1)ではなく、なんかのオブジェクトにぶつかる位置を保持して、ミラーなら何回かたどる「ほぼO(1)」で十分だったよう(ミラーを含むビームの数が少ないため)。
「焼きなましの更新の仕方」は、これまで「状態更新→スコア計算→悪化なら状態戻す」しか書いていなかったので、その先の「スコア計算→良化なら状態更新」があるのは初知見だった。(受理率が悪い場合、ほとんどが悪化して状態を戻す操作をしてしまうので、効果的)
評価関数の変化
二次色の1色だけ光っている場合について、そのまま計算すると「0→-10→+30」となって谷を超えないといけない。
自分は「スコア」を保持して差分を計算してしまっていたため、1色だけ光っているときの悪化を徐々に変化させる方法がうまく取り込めなかった。
ただ、これは簡単に修正できそうで、「スコア」ではなく「クリスタルの状態ごとの個数」を保持してスコア計算を都度行えば、そんなに計算時間かけずに再計算できそうだった。(期間中はこれに気づけず、前半後半にわけるしか思いつかなかった)
その他の工夫
- 最上位陣は、マス全体の焼きなましの他に、小さいエリアの焼きなましを行っていたらしい
- 小さいエリアの焼きなましの場合は、改善するものだけ保持し続けることがキモ?
- 回転数を稼げたり、キャッシュフレンドリに行えたりもする
- 細かい部分での改善が多かったので、小さいエリアで考えるのがよかったよう
- 小さいときの多点スタート
- 試したけど回転数が足りておらず、あまり改善が見られなかったので不採用してたけど、最終結果見ると小さいケースでも探索しきれてなさそうなスコアだったので、ちゃんと検証すべきだったかも
- ビジュアライザの仕方工夫
- 焼きなましのデバッグが辛かったので簡易にできるもの用意しておきたい
- パラメータチューニング工夫
- 評価関数のなだらかな変化
yukicoder No.5002 stick xor
問題
NxNの2次元グリッドが与えられ、各セルは白または黒で塗られている。
このグリッドに対して、以下の操作をK回行う。
i回目の操作では、グリッド内の1xL[i]またはL[i]x1の長方形セルに対して白黒を反転させることができる。
スコアを「(最終状態でのグリッドでの白のセル数) - (最初のグリッドの状態での白のセル数)」とするとき、これを最大化せよ。
- N = 60
- K = 500
- 1 <= L[i] <= 25
最終的に提出したアプローチ
- K個を、順番に、全セルの中で評価値が一番高いところに置いていく
- 評価値は、白にできるマスなら+1点、黒にするけど、その両端が黒なら+0.5点、そうじゃない黒にする場合は-10点
- 次に、適当な場所に長方形セルを動かして良くなるなら採用する山登りを時間いっぱいまで行う
振り返り
初日
制約が1秒しかないので、「評価関数を作って一番評価値がいいところに置いていくgreedy」がよいのでは?と思い実装。
開始1時間ちょいぐらいで、これが最初にしては良いスコア(40,769点)だったので一旦提出。(最終提出の前半部分の方法)
焼きなまし
よくよく考えてみると、時間は短いけど、長方形セルがあまり大きくないので、それを動かすような近傍である程度の回数回せるのでは?と思い、ランダム初期配置+適当なセルに移動してみる焼きなましを実装。
ただ、やってみると1秒ぐらいでは数百万回程度しか回らず、提出してみるも40,307点。
他の手法を考える
上位陣が50000点近くを出しているので、何か別アプローチがよいのかなと思ってしまったため、マッチング問題にできないか?やgreedy、ビームサーチ、グリッドの切り方など考えてみるも、うまくいかず。
最終提出
結局、良い初期状態から温度を下げた焼きなまし(実質山登り)が現状一番よかったので、初日のアプローチ+山登り(温度を下げた焼きなまし)のコードで最終提出。
反省
近傍の作り方で焼きなましは大きく性能が違うので、そこらへんの違いを強く意識したい。。。
今回やってしまった「長方形をランダムな場所に移動」近傍は、後半のほとんど白が多い盤面では大きく悪化させるケースが多く、よい近傍とはいえなかった。
参加されてた方の感想戦やブログを参考にメモしておくと、今回有効な近傍そうだったのは
- 位置を1ずらす
- 長さが違う2つの長方形を入れ替える(近い長さ、長さが1違うもの同士)
- 長さLの長方形をL=la+lbと見なして、それと交換
- 再配置するにしても、greedyに良い配置を見つけてそれを近傍とする
変化量が小さい近傍の方がよさそうで、できれば1や2だけ変化させられる近傍が作れないか考えたい。
それ以外にも、
- 長さが短いものは直接的な改善に使えるので、取っておいて最後に配置
などは気づけるようにしたい。
あと、焼きなましでなく、探索で高スコア出している方もいてすごい。
codeFlyer C. 徒歩圏内
問題
N個の都市が直線上に並んでおり、それぞれの座標Xが与えられる。
都市iと都市jについて、2都市間の距離がD以下なら徒歩、そうでなければ電車で移動する。
このとき、都市の3つ組(i,j,k)で、以下を満たす個数を求めよ。
- i < j < k
- 都市iと都市jの間と、都市jと都市kの間は徒歩で移動
- 都市iと都市kの間は電車で移動
制約
- 3 <= N <= 10^5
- 0 <= X_i <= 10^9
- X_i < X_{i+1}
- 0 <= D <= 10^9
解法
条件の3番目だけ「i,k間の距離がDより大きいもの」になっていて、列挙が難しい。
そこで、条件の1番目と2番目を満たすものの中で、3番目の条件を反対にした「i,k間の距離がD以下のもの」を求めて、前者から除くことを考える。
条件の3番目を反対にした「i,k間の距離がD以下のもの」は、しゃくとり法の要領でO(N)で求めていける。
今、iから見てkが「距離D以下で一番遠いところ」だとして、この間の(k+1-i)個から2個選ぶと、その距離はD以下なので、(k+1-i)_C_2を足していけば求められる。
条件の1番目と2番目だけを満たすものは、同様に、しゃくとり法をしながら求めていける。
今、jから見てkが「距離D以下で一番遠いところ」だと計算していたとして、iから見てjが「距離D以下で一番遠いところ」となるようなiは、そのようなi,jのペアを(j,k)を求めるより前に求めているはずなので、memo[j] = iのようにメモして置く(しゃくとり法のs,tで言う所のtの更新whileの中で)。
そうすれば、条件を満たすものは、(j-i) * (k-i)なので、これを足していけば求められる。
どちらもO(N)で求められるので、全体の計算量はO(N)。
GCJ18 Round1B B. Mysterious Road Signs
問題
西から東に向かって無限に長い直線道路のある場所にSignfieldという町がある。
この町から東に向かってS個の道路標識がある。
i個目の道路標識はD_iキロメートル地点にあり、西側から見て表側がA_i、裏側がB_iという整数が書かれている。
この整数は、それぞれの方向に向かうドライバーのための「目的地までの距離」を表すと考えられているが、そうなっていない場合がある。
それを確かめるため、以下の条件を満たす標識集合の最大数、および、その最大数となる標識集合の数を答えよ。
- 標識集合は、連続する部分集合になっている
- その標識集合内のすべての標識において、「D_i + A_i = M」または「D_i - B_i = N」のどちらか片方を満たすM,Nが存在する
Case#3の場合、1~3番目の標識はM=4、4~5番目の標識はN=2を満たすので、すべての標識が条件を満たし、サイズが5の標識集合はこれ一つなので、答えは「5 1」になる。
# 形式 # S # D_i A_i B_i 5 1 3 3 2 2 2 3 1 1 4 2 2 5 3 3
制約
- 1 <= テストケース数 <= 60
- 1 <= S <= 10^5
- 1 <= D_i <= 10^6
- 1 <= A_i, B_i <= 10^6
解法1
平方分割の古典的な適用例。O(SlogS)解。
標識を順に並べた列を考えた時、その列の真ん中の標識xを「含む」か「含まないか」を考える。
「含む」場合は、標識xの左右に条件を満たすだけ範囲を広げて最大数を見つければ良い。
「含まない」場合は、「0〜x-1までの範囲」か「x+1〜S-1までの範囲」に答えがある可能性があるので、狭めた範囲で同様に含む場合と含まない場合を再帰的に計算する。
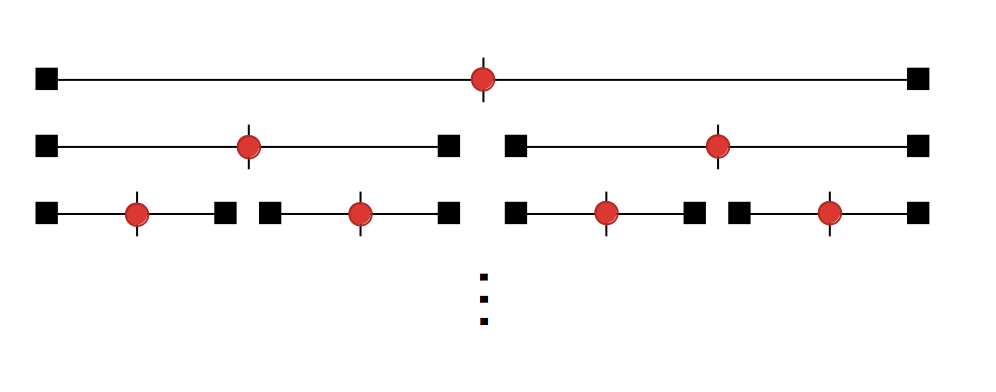
平方分割(再帰関数)の計算量は、Master theorem(分類定理)で求められるらしく、O(SlogS)。
分類定理(master theorem) - LifeTimeException@hrk623
解法2
線形解。
標識を順番に処理していくことを考えて、i番目までの処理結果を使ってi+1番目を高速に処理できないか?を考える。
各標識について、西側から候補地M,Nそれぞれの位置を求めて、並べる。

これを順番に処理することを考える。
まず、一番左の「M=6, N=-1」があった場合に、次の「M=8, N=-1」を考える。
M側は違うMなので、連続する範囲としたいならば、Nで条件が満たされているようにしなければならない。したがって、"M=8, N=-1で連続する"という条件であれば標識数を2とできる。
N側を見ると、一つ前も同じNなので、"M=*, N=-1で連続する"という条件であれば標識数を2とできる。
続けて「M=7, N=0」を考える。
M側は一つ前で"M=8, N=-1で連続する"なら長さ2であることがわかっていて、Mが異なるので、N側の"M=*, N=-1で連続する"なら長さ2の方から繋ぐ必要がある。
なので、M側は"M=7, N=-1で連続する"なら長さ3とできる。
N側は、一つ前がN=-1で異なるので、M側から繋ぐ必要がある。
一つ前のM側は"M=8, N=-1で連続する"なら長さ3で、Nは0ではないので、N=-1になっていた(一番右側の)地点より右側から連続しはじめた、と求める必要がある、。
ここでは最後の-1の地点はi=0のところなので、i=1から連続したとして、条件を"M=8, N=0で連続する"なら長さ2、と更新できる。
これを繰り返していけばよく、保持しておく必要があるのは、M側、N側それぞれで、
- M側はどの位置(数値)で連続しているか?その値
- N側はどの位置(数値)で連続しているか?その値
- 連続している始まりのインデクスstart
- 今見ている側だけで今何個連続しているか?(その開始位置xstart)

を持っておけば、順番に高速に計算できる。
M, Nそれぞれの側で上の情報を保持しておき、i番目からi+1番目を求める時O(1)で、標識数だけ処理するので、計算量全体でO(S)でも求められる。
部分点解法
- S <= 100の場合
- 愚直に、連続する部分集合を決めて条件を満たすかどうかをチェックしてあげればよい。計算量はO(N^3)
GCJ18 Round1B A. Rounding Error
問題
無数にあるプログラミング言語について、N人に、どの言語が好きか?を聞いた。
今、途中までの集計結果(C_1,...,C_L)が与えられている。
例として、「1 2」という集計結果は、3人に回答してもらっていて、言語1が好きといった人が1人、言語2が好きといった人が2人、を表す。
ところで、集計結果を報告したいが、パーセント表記で小数点以下を四捨五入したものを用いると、パーセントの合計が正確に100%にならない場合がある。
残りの人の回答によって、最終的なパーセントの合計が最大となる場合の合計値を答えよ。
制約
- 1 <= テストケース数 <= 100
- 1 <= 途中集計での言語の数L < 質問した人数N <= 10^5
解法
直感的に期待されるのは、ある言語xがパーセント表記にすると四捨五入で切り捨てられていたところ、残りの人がそこに投票することで四捨五入が切り上げられるように変わって、最終的な合計値が増えること。
現在の投票数で四捨五入が切り捨てになっているか、切り上げになっているかは、「(100*x)%Nが、ceil(N/2)以上かどうか」で求められる。
ある言語xに、残りの人のうち1人が投票するということは、この「(100*x)%N」のxを1増やすということで、「100%N」だけ増える。
したがって、y=(100*x)%Nとして、0~N-1までのすべてのyについて、ceil(N/2)以上になるまでに何回「100%N」を足せばよいかをメモ化dfsなどで求めておけば、与えられた途中集計結果のうち、加える数が少なくceil(N/2)以上になるものから必要な分を貪欲に投票していけばよい。
すでに切りあがっているものは無視。最終的に余る場合は、ceil(N/2)以上になるように新たな言語に投票していけばよい。
ただし、「100%N」が0になる場合は、どう操作しても変化させられないことに注意。
部分点解法
- N<=25の場合
- 分割数を考えると、N=25でも1958通りしかないので、全パターン列挙して条件を満たすものについて計算できる
- N<=250の場合
- 「dp[a][b] := a個の分割(x_1,...,x_a)において、合計がb、かつ、x_i >= C_iを満たすとき、小数点以下を四捨五入したパーセント合計値の最大値」を考えると、dp[N][N]が答え。計算量はO(N^3)
TCO18 MM R1 RoadsAndJunctions
概要
マラソンはできるだけ参加していきたいお気持ちだったので参加。
問題やスコアリングが微妙らしく、苦情もでてた。
(Unratedにもなりえそうだけど、まあしょうがない)
最終順位は107位(239人参加)でした。
問題
10~100の町があり、これらすべてを道でつなぎたい。
ただし、確率fpで建設に失敗するジャンクションをコストJCで任意地点に設置依頼することができ、もし成功した場合は道をつなぐ選択肢に含めることができる。
スコアを「設置依頼したジャンクション数 * JC + 道の総距離」としたとき、これを最小化せよ。
最終的に提出したアプローチ
振り返り
工夫したつもりでも順位とか下がって最終提出に入れられなかった。
シュタイナー点の候補列挙と使うものの選択
【最終提出に入れたこと】
最小シュタイナー木問題は知っていたので、3点決めてのシュタイナー点を候補とするとよいのでは?と思って「MST作って、その2辺で作れる三角形」と「ランダムに3点選んで三角形」で時間いっぱい山登りを書いたところ、まあまあなスコアがでていたので、それを最初に提出。
そのあと、いい感じの三角形を用意するのに「ドロネー三角形分割」で三角形を決めるように変更し、(回数を稼いでないので)ベター山登りのつもりで焼きなました。
【最終提出に入れなかったこと】
隣接三角形から四角形を使って、(正方形に近い形の場合を想定して)その四角形の対角線の交点と辺で作られる三角形からも候補点を求めたりしたけど、候補点数が多くなりすぎて計算回数をあまり確保できていないところで使うとあんまり効果が得られなかったようなので、最終提出には入れなかった。
焼きなましするのに高速化は口酸っぱく言われてたので考えていたけど、時間伸ばしたりしても改善があんまり見られなかったり、高速化しなくてもそこそこ良い解にたどり着けてしまっていたので、雑な実装のままで終わってしまった。
ただ、回数はある程度確保できるよう、改善率の多い候補点を選ぶようにはしたけど、提出したらスコア下がったのでいれなかった。
ツイッターみてると、クラスカルの差分更新の案やPrim法使うなど、議論されてたので、もっときちんと考えるべきだった。
ジャンクションの多重化
結果がランダムに変化するので、できるだけ分散が小さい方がよいのでは?と思い、考えてた。
【最終提出に入れたこと】
JCが小さく、追加ジャンクション数が多い何個かのテストケースで、ジャンクションの真横にジャンクションを置いて多重化することで何回か実行しても結果がよりよくなることがあるので、そういうケースのために、全部のジャンクションを多重化しても、実際のスコア期待値よりも小さければ多重化する、というのを入れておいた。
【最終提出に入れなかったこと】
各ジャンクション個別にも考えて、ジャンクションごとに一番期待値が小さくなるよう候補点を最大4点まで追加するコードもやってみたけど、スコアがものすごく悪化してしまった。(けど、もしかしたらバグで-1なケースが出ていたから下がったかも)。
実際、fp=0.2でジャンクション数が3個追加の場合、
- 0個失敗=51.2%
- 1個失敗=38.4%
- 2個失敗=9.6%
- 3個失敗=0.8%
ぐらいなので、ほとんどの場合失敗しない。
テストケースが100個や2000個程度(ある程度収束してそう?)だと少なくて、追加するジャンクション数が少ない場合、JCだけコストを費やして失敗したときの保証をかけるより、失敗しない確率に賭けたほうがよいのかと判断して最終提出にはいれなかった。
反省
- コードの書き方
- 雑に書きすぎてるので、書き方を修正したい
- 実験コードなまま提出してしまって、テストが手で確認程度で終わってるので、ちゃんとテスト書きたい
- 後でそのままライブラリに追加できるように書く
- コードの管理方法
- 工夫したい
- 高速化
- 焼きなまし使うわりに高速化をサボって焼きなましの本領を発揮できていない気がするのでちゃんと高速化する
- 評価スクリプトが配布のやつを使ってたせいで時間かかりすぎなので、分散とか高速化の手段を調べておきたい
- 可視化
- 手を動かす時間があんまり取れずにテスターのやつだけだったので、可視化ツール導入したい
- ぐりぐり動かせるよう、診断人さんが使われてたSiv3Dのmacでも使える版OpenSiv3Dをインストールしたのに結局使わず終わった...
ARC097 E. Sorted and Sorted
問題
1からNまでの番号が書かれた白いボールと黒いボールが合わせて2*N個ランダムに一列に並んでいる。
隣り合う2つのボールを交換する操作を行い、以下を達成したい。
- i < jな(i,j)の組に対して、iと書かれた白いボールは、jと書かれた白いボールより左にある
- i < jな(i,j)の組に対して、iと書かれた黒いボールは、jと書かれた黒いボールより左にある
これを達成するために必要な最小操作回数を求めよ。
制約
- 1 <= N <= 2,000
解法
最終状態がどんな形になるか考えてみると、一番左は何色かの1番のボールが置かれることになる。
例えば、一番左が「白1」だったら、その隣は「白2」か「黒1」があり得る。
このように左から順に埋めていくことを考える。
dp[i][w][b] := i番目までで、白はw番まで、黒はb番まで使った場合のswap回数
を考える。
dp[i][w][b]のとき、(i+1)番目に来うるのは白の(w+1)番か、黒の(b+1)番になる。
wとbまで使った状態で、白の(w+1)番が最終状態で(i+1)番目になる操作回数cがわかれば、
dp[i+1][w+1][b] = min(dp[i+1][w+1][b], dp[i][w][b] + c)
で更新できる。黒の方も同様。
だが、このままだとO(N^3)になっている。
これは状態が冗長で、bはiとwから一意に決まるので、dp[i][w]だけを考えればよい。
操作回数cを考える。
以下のような場合で、w=2、b=1まで使った場合、w3を次に持ってくる場合を考える。
b1 w2 b3 w1 w3 b2
w3は5番目にあり、w=2、b=1まで使っている場合、1、2、4番目はすでに左側に操作で移動しているので、3番目のb3が残っており、それより左に操作で持ってこないといけない。
したがって、「p番目より左側で、w以下、b以下の個数」がわかれば操作に必要な回数が求められる。
そこで、「p番目より左側で、w以下の個数」をcntW[p][w]として求めることを考えると、これは累積和を使ってO(N^2)で前計算しておける。黒についても同様。
したがって、cntW[p][w]とcntB[p][b]を前計算でO(N^2)で求めておいて、dp[i][w]をO(N^2)で求められる。
反省
- mapの参照は対数時間かかるので、ループ回数が多い(10^7近く)ときは無視できない
