AGC023 B. Find Symmetries

問題

各マスに文字が書かれたNxNの盤面が与えられる。
この盤面を右にAマス、下にBマスずらした盤面を考える。はみ出る場合は、(N+i,N+j)を(i,j)とする(1-origin)。
ずらした盤面の中で「すべてのi,jに対して、マス(i,j)とマス(j,i)に書かれている文字が等しい」場合、よい盤面とする。
よい盤面になるような(A,B)のペアが何通りあるか求めよ。

制約

• 1 <= N <= 300
• 0 <= A,B < N
• 文字は英小文字のみ

解法

愚直に探索すると、(A,B)のマスのペアごとによい盤面かどうかのチェックをするO(N^2 * N^2) = O(N^4)で、厳しい。
どこか計算をうまく省略できるところがないか？を考える。

まず、ある(A,B)の時の、マス(i,j)とマス(j,i)のペアを考える。
このマスのペアの文字が同じ場合、他の(A,B)の時でも位置を変えて同様にペアになる場合、チェックを省略できる。

3x3の盤面を全列挙(左上が(A=0,B=0)、右下が(A=2,B=2)の盤面)して確認してみると、

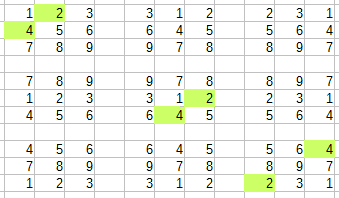
(A=0,B=0)の盤面で位置2,4のペアは、他の(A,B)でもペアになっている場所がある。

ただ、このまま、「ある(A,B)のマスのペアの文字が同じだった場合、別の(A',B')のマスのペアでも文字が同じになる」だけだと、該当する(A',B')にメモりに行く感じになってしまうので、探索する(A,B)が少なくなってもメモりに行く分に変わるだけで計算量は減らない。

ある(A,B)での盤面でのすべてのマスのペアを、他の(A',B')でもペアになっているところを確認してみると、上の図のように、すべて同じ盤面でのペアになっていることがわかる。

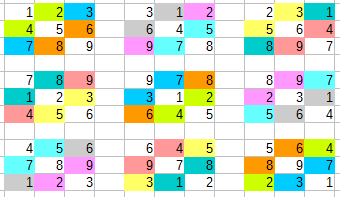
全部のペアを取ってみると、同様で、斜め方向(左上から右下)について、盤面での「マスのペアの集合」は同じになっている。
Nが変わってもこれは変わらず、斜め方向のN個の盤面は、どれか1つの盤面のチェックをすればよいということなので、ひとまとめに計算できる。

よって、「マスのペアの集合」はN種類あり、その集合内のペアがそれぞれ同じ文字のペアになっているかどうかがO(N^2)でチェックでき、成り立つなら答え+=N盤面とできる。計算量はO(N^3)。