三井住友信託銀行プログラミングコンテスト2019 E. Colorful Hats 2

問題

N人が一列に並んでおり、各人は赤、青、緑いずれかの帽子をかぶっている。
そして、左からi番目の人は「自分より左で、自分と同じ色の帽子をかぶっている人はAi人いる」と言っている情報が与えられる。

この情報に基づいた場合、帽子の色の組み合わせとして考えられるのは何通りか、mod1000000007で答えよ。

制約

• 1 <= N <= 100000
• 0 <= Ai <= N-1

解法

0 -> 1 -> 2 -> 3 -> ...とできる取り方は何通りか？という問題と考えられる。
dp的に考えようとすると、ある地点で取れる組み合わせは色を無視すると一意に決まることがわかる。
(「1まで出ているのが2個＆2まで出ているのが1個」のようなもの)

ある地点でAiだった場合、Ai-1までのものがすでに1つ以上出ているはずなので、これがx個だった場合は、Ai-1のx個のうちから1つ選んでAiにするようにすればよく、組み合わせはx倍になる。
これを初期値を1通りとして、上記を繰り返せばよい。
また、色の組み合わせとして、0が1回なら3通り、0が2回または3回ならば6通りの割当があり得るので、それをかければ良い。

この問題では、不正な入力もあり得る。
0が4個以上ある時や、最初が0以外で始まる場合は0通りを返す。
また、途中で不正な入力だった場合は、Ai-1の個数が0個になっているはずなので、0通りを返す。

ABC127 F. Absolute Minima

問題

関数f(x)があり、はじめはf(x)=0として与えられる。
Q個のクエリが与えられ、

• 更新クエリの場合は、f(x) <- f(x) + |x-a|+b
• 求値クエリの場合は、f(x)の最小値とその時のxを出力

を行え。

制約

• 1 <= Q <= 2*10^5
• -10^9 <= a, b <= 10^9
• 1番目のクエリは更新クエリ

解法

与えられた問題は、「min Σ |x-a_i| + b_i」を求める問題と言い換えられる。

ここでb_iは与えられるたびに加算していけば良いので、結局は
min Σ |x-a_i|
をa_iが与えられるたびに高速に求められれば良い。

この答えは、xが「与えられたa_iの中央値」のとき最小値となる。
中央値を高速に管理する手段として、multisetを2つl,r持って、

1. lに値を入れる
2. lよりもrのサイズが2以上大きければlの最大の値をrに移す(サイズを均等にする)
3. lの最大値とrの最大値を比較し、大小関係が逆であれば入れ替える(状態を維持)

というのを繰り返せば、lの最大値が常に中央値になる。

最小にするxがlの最大値で得られるので、そのx_minに対してΣ|x-a_i|を求めることを考える。
x_minより小さいa_iについてはΣ(x-a_i)で、x_minより大きいa_iについてはΣ(a_i-x)となる。
これは、lとrで管理できているので、multisetと一緒に、入っている値の和l_sum, r_sumを一緒に管理しておけば、「(lのサイズ*x_min - lsum) + (rsum - rのサイズ*x_min)」で求められる。
したがって、最終的な答えは、これにΣb_iを足したものになる。

ABC146. E. Rem of Sum is Num

問題

長さNの正整数列A_iと正の整数Kが与えられる。
このとき、Aの空でない連続する部分列で、「要素の和のmod Kと要素数が等しくなるものの数」を求めよ。
ただし、位置が異なる場合は区別する。

制約

• 1 <= N <= 2*10^5
• 1 <= K <= 10^9
• 1 <= A_i <= 10^9

解法

問題を式で表現すると、

(Σ_{i=l}^{r} Ai) mod K = r - l + 1

と書ける。
ここで、左辺の和を累積和S_iに置き換えて考えると、

(S_{r} - S_{l-1}) mod K = r - (l - 1)

と変形でき、整理すると、

(S_{r} - r) mod K = (S_{l-1} - (l-1)) mod K

のようになる。
したがって、l < rで、r-l < Kであるような範囲で、「(S_i - i) mod K」が等しくなるような個数を数える問題になる。

X_i = (S_i - i) mod Kとすると、これは、各iについて、i+K-1までの範囲にあるjについて、X_iと等しいX_jの個数を求めることだが、これは、mapなどで、i+1に移動する際に、X_iを消してX_{i+1}を追加するような操作をすれば、高速に求められる。

全体で、O(NlogK)で高速に求められる。

反省

以前の式変形する問題。

ARC075 E. Meaningful Mean - phyllo’s algorithm note

第一回日本最強プログラマー学生選手権決勝 A. Equal Weight

問題

N個のシャリAとM個のネタBがあり、シャリiの重さはAi、ネタjの重さはBjで与えられる。
ここで、寿司の握りはシャリとネタ1つずつの組み合わせで作ることができ、同じ重さの寿司を2つ作りたい。
これが可能かどうか判定し、可能な場合は組み合わせのインデクスを1つ出力せよ。不可能な場合は-1を出力せよ。

制約

• 2 <= N, M <= 2*10^5
• 1 <= Ai, Bj <= 10^6
• 同じ重さのシャリは存在しない
• 同じ重さのネタは存在しない

解法1

N,Mが大きい時を考える。

シャリとネタの重さの組み合わせは2*10^6までしかないため、鳩ノ巣原理から、それ以上の組み合わせを生成した場合、同じ重さになる寿司が1つは必ず現れる。

したがって、重さをメモりながらシャリとネタの組み合わせを全部列挙するように書くと、2*10^6程度で必ず見つかるか、列挙が終わる。

解法2

Xi := Aの中に重さiのシャリがあるか(1か0)
Yi := Bの中に重さiのネタがあるか(1か0)
と定義し、その畳み込みZi = Σ^i_{j=0} X_j*Y_{i-j}を考えると、
これは「同じ重さiになるシャリ/ネタのペアの個数」になる。

この畳みこみはFFTを行うとO(NlogN)で求められるので、実装次第で通せる。
(doubleで計算していると間に合わなかったけどfloatにすると間に合った。計算精度はわらかない・・・怪しいかも。テストケースによる？)

ABC141 F. Xor Sum 3

問題

N個の非負整数A_iが与えられる。
これを1個以上が属する2つのグループにわける。
各グループ内の整数のすべてのxorを取ったものの和を最大化するような選び方をした場合、その最大値を返せ。

制約

• 2 <= N <= 10^5
• 0 <= A_i < 2^60

解法

すべての与えられた整数のxorを取ったものをsとする。
このとき、各ビットごとに見ると、

• 1になっている→2つのグループにどう分けても1の数が奇数個なので、関係ない
• 0になっている→グループの選び方によっては、0と0、または1と1にできる

となっていることがわかる。

なので、sのビットが0になっている部分で1と1を作れるほど桁上りが発生して値を大きくできる。また、そのようなビットは上の桁でできるほど値がおおきくなりうれしいので、上の桁から1と1が作れるようにグループを作りたい。

最終的な答えは、「(sの1になっている部分のxor)＋(sの0になっている部分でできるだけ上位の桁から1と1に分けた場合のグループのxor)*2」になる。
前者はすぐ作れるが、後者はどうやったら求められるか？が問題。

sの1になっている部分を0につぶしたA_iを、B_iとする。
ここで、B_iのビット列を縦に並べた行列を考える。

入力例1の(3,6,5)の場合、
0 1 1
1 1 0
1 0 1

この行列において、いくつかの行を選んでxorを取ったもの＝片方のグループになる。
B_iは全部のxorを取ると0になるため、選ばなかったもののグループのxorは選んだもののグループのxorと同じになる。
したがって「Bからいくつか選び、それらのxorの最大値」を求めたい、という問題になる。(0個または全部選ぶ場合はxorは0なので、無視して考えても問題ない)

これは、xorの掃き出し法を使うと求められる。
あるB_iに対して、B_j (i!=j)とのxorを取ると、B_iは(B_i xor B_j)になるが、それはB_iとB_jを選んだとき(「iとjを選ぶ行為」とxorを取った後で「iを選ぶ行為」が同じ)の値になり、(B_i xor B_j)とB_jを選んだ場合は、B_iだけを選んだとき(「iだけを選ぶ行為」とxorを取った後で「iとjを選ぶ行為」が同じ)の値になる。
このように行に対してxorを取る操作は、対応関係が取れるので、各ビットで1になっているものが1つだけになるように行のxorを取れば、「そのビットにおいて、1が立っているものを選んでおけば、他の0になっているものをどのように選んでもよい」とできる。
これを上位の桁から掃き出し法で行っていく。(1がどれも立っていないビットの場合は何もできないので無視)
最終的に、全部の行のxorを取れば最大値が得られる。

ABC139 F. Engines

問題

N個の2次元ベクトルが与えられる。
ここからいくつか選んだ和のベクトルの大きさの最大値を求めよ。

制約

• 1 <= N <= 100
• -1,000,000 <= x_i, y_i <= 1,000,000

解法

答えとなるベクトルの向きを固定して考える。
このとき、この向きに寄与するベクトルは、その向きの成分が正となるベクトル(±90度までにあるベクトル)だけを集めてきたときの和になる。

なので、角度でベクトルをソートし、角度が180度分の範囲にあるベクトルをすべて足し合わせた中で一番大きさが大きくなるものを答えればよい。

または、より簡単に、連続区間をすべてチェックしても間に合うので、O(n^2)またはO(n^3)でもよい。

ABC137 E. Coins Respawn

問題

1からNまで番号がついたN頂点M辺の有向グラフが与えられる。
頂点1から頂点Nまで辺を辿っていくことを考える。
辺iは通過するのに1分かかり、通るたびにコインがCi枚もらえる。
頂点Nにたどり着いておいてあるボタンを押すと「それまで回収したコインの総数から経過時間*P枚を引いたコイン枚数」が得られる。
(コインが足りない場合は0枚になる)
得られるコインが最大になるように行動した場合、何枚得られるか？
最大値が存在しない場合は-1を返せ。

制約

• 2 <= N <= 2500
• 1 <= M <= 5000
• 1 <= Ai, Bi <= N
• 1 <= Ci <= 10^5
• 0 <= P <= 10^5
• 有向グラフは1からNまで到達可能

解法

最長経路は辺のコストの正負を逆転させることで最短経路と同じ要領で求められる。
ただし、ループがあると最大値が無限に大きくできてしまうため、それを検出できるベルマンフォードで適用を考える。

単純に適用しようとすると、サンプルにある通り、「頂点1からたどり着けない頂点」、「頂点Nにたどり着けない頂点」も含めて閉路を検出してしまう。
なので上記のたどり着けない頂点をチェックして、その頂点を除いたグラフで適用すれば良い。

反省

「たどり着けるか？」の頂点のチェックにdfsではなくbfsで書いてしまったが、

queue<int> que;
while(!que.empty()){
  int x = que.front(); que.pop();
  visit[x] = true;
  FOR(it, g[x]){
    if(visit[it->dest]) continue;
    que.push(it->dest);
  }
}

のように書いてしまうと、O(N^2)で、
1->2, 1->3, ..., 1->N, 2->3, 2->4, ..., 2->N, ..., N-1->N
のようなグラフでTLEになってしまう。

AGC036 A. Triangle

問題

整数Sが与えられる。以下の条件をすべて満たす6つの整数X1,Y1,X2,Y2,X3,Y3を1組求めよ。

• 0 <= X1, Y1, X2, Y2, X3, Y3 <= 10^9
• 二次元平面上の3点(X1, Y1), (X2, Y2), (X3, Y3)を頂点とする三角形の面積がS/2

制約

• 1 <= S <= 10^18

解法

変数が多いので、1点を固定して考える。(X1, Y1) = (0, 0)とする。

ここで、三角形の面積を求める方法を調べると、「直交座標による式」が出てくる。
三角形 - Wikipedia

面積 = |X2*Y3 - X3*Y2| / 2

これが2点の関係式になるので、これを満たす2点を探す。

例えば、(X2, Y2) = (10^9, 0)としてみると、S = 10^9*Y3である必要があるが、Sが10^9で割り切れないといけない。
しかし、(X2, Y2) = (10^9, 1)とすると、S = 10^9*Y3 - X3となり、これはY3を「Sを10^9で割った切り上げ」とすると、X3 = 10^9*Y3 - Sとなる。

これは以下のようになっている。(解説放送より)

ABC134 F. Permutation Oddness

問題

1からNまでの順列pの「奇妙さ」を「Σ_{i=1}^N |i - p_i|」と定義する。
奇妙さがkであるような順列の個数の10^9+7で割った余りを求めよ。

制約

• 1 <= N <= 50
• 0 <= K <= N^2

解法

「1からNを並べたもの」と「順列p」のペアを考える。
順列pでの数字を線でつないで表現すると以下のように書ける。

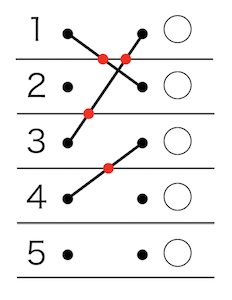
この場合、右側の順列pは{3, 1, 4, ?, ?}に対応する。

ところで、問題の「奇妙さ」は、「数字の間に引いた線」と「ペアの線」の交点(赤色の点)の数で考えることができる。
これを元にDPを考える。

そのまま考えると、つないでいない点を保持する必要がありそうでbitDPになりそうだが、以下のように考えると、点の個数だけ保持すれば良くなる。

状態は、
dp[i][j][k][l] := iペア目までで、まだつないでいない左側の点がj個、まだつないでいない右側の点がk個、ここまでの奇妙さの合計がlである順列の個数
だが、jとkは実は常に同じになり、片方だけで良いので、
dp[i][j][k] := iペア目までで、片側でまだつないでいない点がj個、ここまでの奇妙さの合計がkである順列の個数
となる。

遷移は、配るDPで考えると、dp[i][j][k]について、(i+1)ペア目をどうするかで4パターンありえる。

1. 両方共、点を繋がない
   • 横線と交差する点は2*(j+1)個になるので、dp[i+1][j+1][k+2*(j+1)] += dp[i][j][k]
2. (i+1)ペア目同士を繋ぐ
   • 横線と交差する点は2*j個になるので、dp[i+1][j][k+2*j] += dp[i][j][k]
3. (i+1)ペア目の片方を、iペア目以前の繋いでない点のどれかと繋ぐ
   • 横線と交差する点は2*j個になるが、iペア目以前のどれに繋ぐかでj通り、どちら側かで2通りなので、dp[i+1][j][k+2*j] += dp[i][j][k] * 2*j
4. (i+1)ペア目の両方を、iペア目以前の繋いでない点のどれかと繋ぐ
   • 横線と交差する点は2*(j-1)個になり、iペア目以前のどれに繋ぐかが左右でj通りずつあるので、dp[i+1][j-1][k+2*(j-1)] += dp[i][j][k] * j*j

初期値はdp[0][0][0] = 1通りで計算すればよい。
答えはdp[N][0][K]になる。

これは、箱根駅伝DP(箱根DP)とも呼ばれるらしい。
Hakone | Aizu Online Judge

yukicoder No.848 なかよし旅行

問題

N個の町がM本の道でつながっており、道の移動にかかる時間が与えられる。
今、2人が町1にいるが、T分以内に町Pと町Qを回って町1に戻ってきていなければならない。
町Pと町Qは2人のうちどちらか1人でも回ればよい。
ただし、道の途中で引き返すような行動はとれない。

2人はできるだけ一緒に行動したいが、最大で何分一緒に行動できるか？
不可能な場合は-1を出力せよ。

制約

• 3 <= N <= 2000
• 2 <= M <= 10^5
• 2 <= P <= Q <= N
• 1 <= T <= 10^9
• 1 <= ある道の移動時間 <= 10^9
• すべての町は町1から歩いていくことができる

解法

まず、全部一緒に回れるかどうかを考える。
1->P->Q->1と一緒に回る時間がT分以下だった場合、適当に待ち時間を入れることで答えをTにできる。

上記でない場合は、何分かの間、別行動が発生する。
別行動をしている時間をtとすると、答えはT-tになる。

ある頂点xまで行って、それぞれP,Qに別々に移動して、xに戻ってくることを考えると、x->P->xかx->Q->xの長い方の時間だけかかる。
しかし、例えば、x->Pが1、x->Qが10のような場合、x->Q->xの20だけかかるが、P->yが10、Q->yが1のようなyが存在する場合、x->P->yとx->Q->yが11ほどとなり、y->1が1->xと同じでもそのルートを通った方が短くなる。

したがって、x,yのペアをすべて確認し、t={x->P->yかx->Q->yの長い方}として、T-tで一番長いものを求めればよい。

反省

さっと思いつくgreedyの「同じ場所xに戻る」のが嘘解法だというのに気付くのが難しい、、、

M-SOLUTIONS プロコンオープン C. Best-of-(2n-1)

問題

高橋くんと青木くんが、どちらかが合計N回勝つまでゲームを繰り返す。
1回のゲームでは、高橋くんが勝つ確率はA%、青木くんが勝つ確率はB%、引き分けになる確率はC%である。

ゲームが行われる回数の期待値を出力せよ。
ただし、期待値は小数ではなく、互いに素なP,Qを用いて期待値がP/Qと表せるとき、R*Q=P (mod 10^9+7)となる整数Rで答えよ。

制約

• 1 <= N <= 10^5
• 0 <= A,B,C <= 100
• 1 <= A+B
• A+B+C = 100
• 入力はすべて整数

解法

(解説の方法)
Nの制約からO(N^2)な解法は許されない。

まず、引き分けについて考える。
引き分けは、そこまでのゲーム内容とは無関係にC%の確率で起こる。
そのため、勝ち負けが決まるようなゲームの内容に依存せずに考えられる。

依存するのは、勝ち負けが決まるようなゲームの回数で、これがM回だった場合、引き分けの回数の期待値が求められる。(ゲームを遅滞させていると考えられる。どのぐらい遅滞させるか？)
これは、「勝ち負けが決まるゲームが行われる確率が(100-C)/100、引き分けになるゲームが行われる確率がC/100のとき、勝ち負けが決まるゲームがM回行われる場合の、ゲームの行われる回数の期待値は？」という問題と考えられる。
これは、E_{勝ち負けが決まるようなゲームの回数}を残り何回ゲームを行うか？の期待値として、1回分だと、

E_0 -> E_1
↓↑

のような遷移であり、
E_0 = 1 + (100-C)/100 * E_1 + C/100 * E_0
E_1 = 0
と書けるので、
E_0 = 100/(100-C)
となる。
M回分で考えると、E_M = M * 100/(100-C)となる。
よって、勝ち負けが決まるようなゲームの回数がM回の場合、引き分けも含めて行われるゲームの回数の期待値は「M * 100/(100-C)」回である。

あとは、勝ち負けが決まるようなゲームの回数がM回であるような確率を求められれば、上記の回数に掛けることで全体の期待値を求められる。

勝ち負けが決まるゲームで考えた場合、N回以上2N回未満の回数で勝負が決する。
これをM回と置くと、M回のうち、高橋くんが勝つケースでは、M回目は高橋くんである必要があり、M-1回目までで高橋くんがN-1回勝っている必要がある。
これは、組み合わせを用いて、{M-1}_C_{N-1} * (A/(A+B))^N * (B/(A+B))^{M-N}の確率で起きる。
青木くんについても同様で、{M-1}_C_{N-1} * (B/(A+B))^N * (A/(A+B))^{M-N}の確率で起きる。
よって、上記の2つを足し合わせたものが、M回で勝負が決する確率になる。

あとは、MをN～2N-1でループを回し、Mの時の確率と上記の期待値をかけたものを足し合わせていけばよい。
(mod_conv, mod_inverse, mod_powあたりが必要)

反省

コンテスト中はO(N^2)な解法から計算量を落とそうと考えて、ごちゃごちゃいじっていたら終わってしまった。。。

O(N^2)の解法は、
E_{x,y} := 高橋くんの勝ち数がx、青木くんの勝ち数がyのとき、ゲームの残り回数の期待値
と考えると、

E_{x+1,y} <- E_{x,y} -> E_{x,y+1}
               ↓↑

のような遷移になっていて、再帰的に、
E_{x,y} = 100/(100-C) + A/(A+B) * E_{x+1,y} + B/(A+B) * E_{x,y+1}
E_{N,*} = E_{*,N} = 0
E_{0,0} = ?
と書ける。
(引き分けの部分も依存してしまっていて分離できなかった)

ABC128 F. Frog Jump

問題

N個の蓮が一列に並んでおり、0～N-1まで番号がついている。
最初、0の蓮におり、以下の手順に従ってゲームを行う。

1. 正の整数A, Bを決める。得点は最初は0。
2. 現在の位置xとして、y=x+Aとする。xの蓮を消してyに移動する
このとき、y=N-1ならゲーム終了。そうでなく、yの蓮があるなら得点s_yを得る。yの蓮がない場合は得点を10^100減らして終了。
3. 現在の位置xとして、y=x-Bとする。xの蓮を消してyに移動する
このとき、y=N-1ならゲーム終了。そうでなく、yの蓮があるなら得点s_yを得る。yの蓮がない場合は得点を10^100減らして終了。
4. 手順2に戻る

最終得点をできるだけ大きくしたい場合、最終得点はいくらになるか。

制約

• 3 <= N <= 10^5
• -10^9 <= s_i <= 10^9
• s_0 = s_{N-1} = 0

解法

問題文から以下がわかる。
経路の動きとしては「0 -> A -> A-B -> 2A-B -> 2A-2B -> ... -> N-1」のように推移する。
また、手順3ではN-1に達することはできないので、手順2の時にN-1にたどり着くように終わらないといけない。よって「(x+1)*A-x*B = N-1」となるようなxがある。

単純にA,Bをループで回すとxはO(1)で決まるが、スコアの計算にO(N)かかってしまう。全体としてはO(N^3)で間に合わない。

ここで、「(x+1)*A-x*B = N-1」を変形して「x(A-B)+A = N-1」と考えて、xとA-Bでループを回すことを考える。(これに気付くためにはAとx、Bとxとかも考えていればたどり着ける？)

C=A-Bとして、これはループを回すとして固定して考える。
x=1からループを回すと、AとBが決まるので、どういう蓮を通っているかを表示してみると、左右からCずつx個取るような対称形の法則性がでてくる。

この法則性を活用すると、取る蓮が同じになるようなものをまとめて、かつ、xを順番に増やすことで効率的に求めていける。

気を付けることとしては、
・x*Cが範囲を超えないようにする
・A,Bの条件をちゃんと満たすかチェックする
・左右から取っていったときに、すでになくなった蓮だった場合は条件を満たせないので、すでに取った蓮かどうかを記録しながらxを増やしていく

Cとxのループは、ΣN/iのような形になるのでO(NlogN)の計算量になる。

メモ

• 取れる形は対称となる
  • ちょうどゴールしないといけないので、スタート直後は+A、ゴール直前は+Aで、A,Bの繰り返しなので対称な形になる
• スタートからA-Bずつ進む、ゴールからA-Bずつ戻る
  • 対称な形を維持して左右からA-Bだけ取るような形を作れる
• A-Bを何回行うか？を決めると、対称でないといけない制約からA,Bが決まる
• A-Bと、A-Bが何回か？をループで回せばよい
  • 何回か？は調和級数の形からO(NlogN)

ABC128 E. Roadwork

問題

東西に無限に続く1本の大通りがあり、数直線とみなせる。
大通りでN回の工事が行われ、i番目の道路工事はSi-0.5からTi-0.5の時刻にXi地点を通行止めにする。
Q人の人が座標0におり、i番目の人は時刻Diで出発し、速度1で進む。
しかし、工事中の通行止めの地点に到達するとそこで止まる。
各人の進む距離を求めよ。無限に進む場合は-1を返せ。

制約

• 1 <= N, Q <= 2*10^5
• 0 <= Si < Ti <= 10^9
• 1 <= Xi <= 10^9
• 0 <= D1 < ... < DQ <= 10^9
• 同じ地点で複数の工事が時刻が重なるように実施はされない

解法1

各工事について、いつ出発すればその工事地点で止まることになるかを考える。
これは簡単で、[Si-Xi, Ti-Xi)の時間に出発する人がこの工事地点で止まりうる。
ただし、複数の工事がある場合は、一番Xiが小さいところで止まる。

範囲更新できればよいので、座標圧縮したものに対して遅延セグメント木でXiが大きい方から入れていき、小さい時刻から人の出発時刻とセグメント木の値を見比べて答えていけばよい。

(座圧の時に、各人の時刻も一緒にいれておくと、簡単に問い合わせできる)

解法2

遅延セグメント木ではなく、setを使って求めることができる。

setに各人の時刻を入れておき、工事のXiが小さい方から、[Si-Xi, Ti-Xi)の範囲にある人を取り除いていけばよい。
Si-Xiをlower_boundで探して、イテレータを回してTi-Xi未満の人をeraseしていく。

類題

atcoder.jp

Chokudai SpeedRun002 J. GCD β

問題

整数のペアがN組あり、i番目の整数のペアは(Ai, Bi)で与えられる。
すぬけくんは各ペアからちょうど1つずつ整数を選んで、選んだN個の整数の最大公約数として考えられる最大値が何になるか知りたい。

制約

• 1 <= N <= 5*10^4
• 1 <= Ai, Bi <= 10^9

解法

最初にA1かB1の約数の集合を考えると、A2かB2の約数の集合と共通する約数のみを残していくイメージをすると、どんどん集合サイズが減っていくイメージになる。
なので、結局、最初のA1かB1の約数の集合が最大サイズで、この約数だけが答えの候補になっている。
10^9以下の整数の最大の約数の数を持つものでも1344個程度(高度合成数)しかないので、A1とB1の約数を列挙して合わせて、その約数から条件を満たせるものを選べばよい。

Chokudai SpeedRun002 I. カツサンドくんβ

問題

N種類の食べ物があり、食べ物iの体力がAi、攻撃力がBiで与えられる。
この食べ物同士を戦わせ、最強の食べ物を決めたい。

最強の食べ物は、以下のような対戦を行ったとき、どの他の食べ物と戦っても勝利できるような食べ物とする。

食べ物iと食べ物jが対戦する場合、以下のような流れで行われる。
1. 互いに攻撃する。このとき食べ物iの体力はBj減り、食べ物jの体力はBiだけ減る。
2. 体力が0以下になった食べ物が戦闘不能になる
3. いずれの食べ物も戦闘不能になっていない場合は1に戻る
4. 両方が同時に戦闘不能になったら引き分け、片方のみが戦闘不能ならもう片方を処理とする

最強の食べ物を求めよ。

制約

• 1 <= N <= 2*10^5
• 1 <= Ai, Bi <= 10^9
• 入力される値はすべて整数

解法

最強の食べ物が存在する場合は、どう戦っても必ず勝つはずなので、N種類の食べ物が順番に現れて勝ち抜き戦をするような感じで求めればよい。
引き分けの場合は、いったんどちらかを選んでおく。
最後に勝ち抜いた食べ物が最強候補だが、引き分けの食べ物があったかもしれないので、最後に、他のすべての食べ物に勝てるかチェックすればよい。

解法2(未証明)

勝敗判定を考えると、iとjが戦った場合にiが戦闘不能になるまでのターン数は(Ai+Bj-1)/Bj)-1?回なので、iが勝つには「floor( (Ai+Bj-1)/Bj ) > floor( (Aj+Bi-1)/Bi )」である必要がある。
floorを外して小数考えると、整数部分が違う場合はただしく不等号比較ができているが、整数部分が同じ場合にfloorでは等号になるものが不等号の比較になってしまう。
これは、本当は引き分けなのに、どちらか優劣をつけることになるが、上記の解法でのいったんどちらかが勝ち残るのと同じ感じになる。
floorを外して小数で考えて、移項して整理すると「(Ai - 1)*Bi > (Aj - 1)*Bj」である必要がある。
したがって、(Ai-1)*Biでソートしたときに一番大きい値になるものが最強候補といえるので、他のすべての食べ物に勝てるかチェックして答えを求めればよい。